4.
Ein Rechendreieck besteht aus ganzen Zahlen grösser als 0. Nebeneinander liegende grauen Dreiecke werden addiert, um den Wert des weissen Dreieck zwischen ihnen zu erhalten.
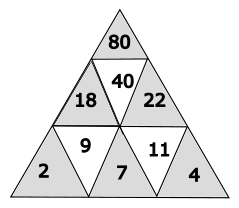
Der Wert des weissen Dreiecks muss verdoppelt werden, um die Zahl im darüberliegenden grauen Dreieck zu berechnen. Das Rechendreieck darf nur ganze Zahlen enthalten. Hier hast du ein Beispiel
eines Rechendreiecks.
a) Ergänze die fehlenden Zahlen im untenstehenden Rechendreieck. Gib als Endresultat die Zahl im rot umrandeten Dreiecken an.
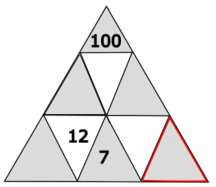

a) Ergänze die fehlenden Zahlen im untenstehenden Rechendreieck. Gib als Endresultat die Zahl im rot umrandeten Dreiecken an.

Welche Zahl gehört in das gelb markierte Dreieck?
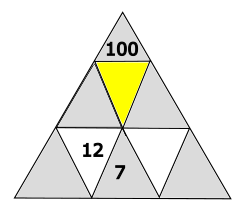

- 200
- 50
- 40
- 60
Der Wert im gelb markierten Dreieck beträgt 50.
Um auf 100 zu kommen muss das darunterliegende weisse Dreieck verdoppelt werden. 50 \(\cdot\) 2 = 100.
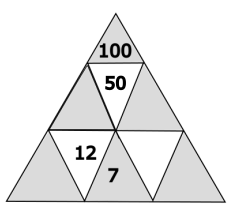
Welche Zahl gehört in das blau markierte Dreieck?
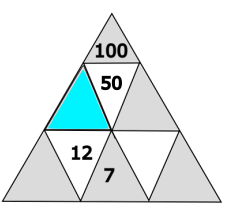

- 30
- 20
- 12
- 24
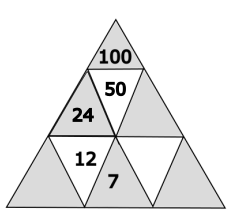
Der Wert im blau markierten Dreieck beträgt 24.
Das darunterliegende weisse Dreieck hat den Wert 12. Es muss verdoppelt werden um auf das blaue Dreieck zu kommen. 12 \(\cdot\) 2 = 24.
Welche Zahl gehört in das gelb markierte Dreieck?
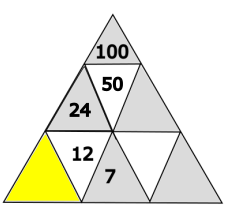

- 3
- 5
- 10
- 7
Das gelbe Dreieck hat den Wert 5.
Berechnung: 12 - 7 = 5
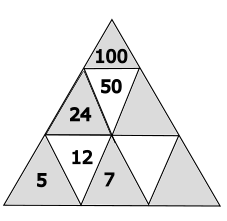
Welche Zahl gehört in das gelb markierte Dreieck?
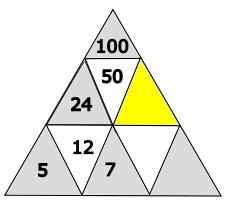

- 19
- 29
- 16
- 26
Das gelbe Dreieck hat den Wert 26.
Berechnung: 50 - 24 = 26
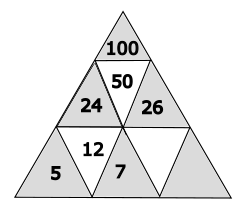
Welche Zahl gehört in das gelb markierte Dreieck?
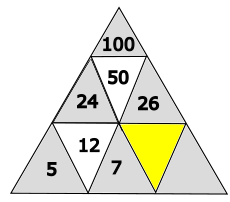

- 14
- 12
- 8
- 13
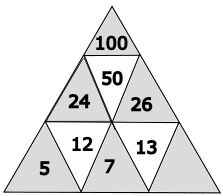
Die Zahl im Dreieck beträgt 13. Das berechnest du, indem du 26 : 2 = 13 rechnest.
Das letzte, untere Dreieck muss den Wert 6 haben, denn 6 + 7 = 13.
Endresultat
- 9
- 4
- 12
- 11
- 7
- 5
- 6
- 13
b) Ergänze die fehlenden Zahlen im untenstehenden Rechendreieck so, dass das Rechendreieck die folgende Eigenschaften hat:
• Keine zwei Zahlen auf den grauen Dreiecken dürfen gleich sein.
• Das Rechendreieck darf nur ganze Zahlen enthalten
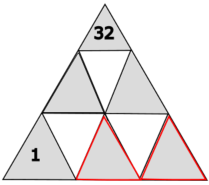
Gib als Endresultat die Werte der rot umrandeten Dreiecke an.
• Keine zwei Zahlen auf den grauen Dreiecken dürfen gleich sein.
• Das Rechendreieck darf nur ganze Zahlen enthalten

Gib als Endresultat die Werte der rot umrandeten Dreiecke an.
Welche Zahl gehört in das gelb markierte Dreieck?
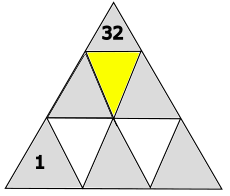

- 11
- 13
- 14
- 16
32 : 2 = 16
Der Wert des gelb markierten Dreiecks beträgt 16.
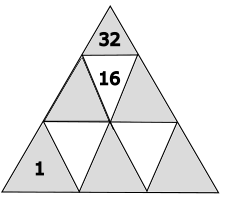
Welche Zahl gehört in das gelb markierte Dreieck und das blau markierte Dreieck?
Möglicherweise musst du hier verschiedene Varianten ausprobieren. Die Zahlen, die du hier wählst, haben eine Auswirkung auf die unteren Ebenen.
Achtung: Keine zwei Zahlen auf den grauen Dreiecken dürfen gleich sein.
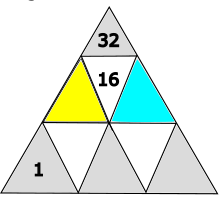
Möglicherweise musst du hier verschiedene Varianten ausprobieren. Die Zahlen, die du hier wählst, haben eine Auswirkung auf die unteren Ebenen.
Achtung: Keine zwei Zahlen auf den grauen Dreiecken dürfen gleich sein.

- gelb = 9, blau = 5
- gelb = 6, blau = 10
- gelb = 8, blau = 8
- gelb = 4, blau = 12
Es gibt nur eine mögliche Lösung: gelb = 6 und blau = 10
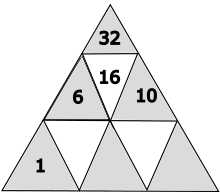
Die folgenden Lösungen sind nicht korrekt:
gelb = 9, blau = 5
nicht korrekt, denn die Zahlen in den darunterliegenden weissen Dreiecken sind keine ganzen Zahlen.
9 : 2 = 4.5 und 5 : 2 = 2.5
gelb = 8, blau = 8
nicht korrekt, denn bei dieser Lösung würden zwei gleiche Zahlen auf den grauen Dreiecken vorkommen (zwei Mal 8)
gelb = 4, blau = 12
nicht korrekt, denn bei dieser Lösung würden zwingendermassen zwei gleiche Zahlen auf den grauen Dreiecken vorkommen (zwei Mal 3 auf der untersten Ebene).
Welche Zahlen gehören in die markierten Dreiecke?
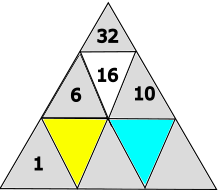

- gelb = 4, blau = 5
- gelb = 3, blau = 6
- gelb = 4, blau = 8
- gelb = 3, blau = 5
gelb: 6 : 2 = 3
blau: 10 : 2 = 5
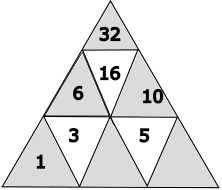
Welche Zahlen gehören in die markierten Dreiecke?
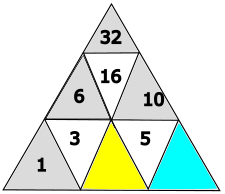

- gelb = 2, blau = 3
- gelb = 3, blau = 1
- gelb = 1, blau = 3
- gelb = 2, blau = 4
gelb: 3 - 1 = 2
blau: 5 - 2 = 3
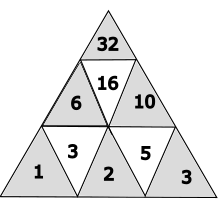
Endresultat
- 1, 3
- 2, 3
- 2, 4
- 1, 4
- 2, 5
- 3, 5
- 4, 5
- 2, 6
