7.
Ein Rechenquadrat besteht aus ganzen Zahlen grösser als 0. Die Zahl
in der Mitte ist die Summe der vier Zahlen in den grauen Dreiecken.
Jede Zahl in einem grauen Dreieck ist die Summe der beiden Zahlen
in den angrenzenden weissen Dreiecken. Hier hast du ein Beispiel
eines Rechenquadrates.
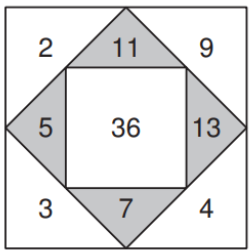
a) Ergänze die fehlenden fünf Zahlen im untenstehenden Rechenquadrat. Gib als Endresultat die Zahlen, die in den grauen Dreiecken enthalten sind an.
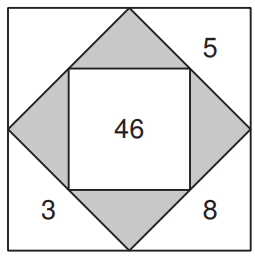

a) Ergänze die fehlenden fünf Zahlen im untenstehenden Rechenquadrat. Gib als Endresultat die Zahlen, die in den grauen Dreiecken enthalten sind an.

Welche Zahlen gehören in die gelben Dreiecke?

- 5 und 3
- 14 und 11
- 11 und 13
- 12 und 15
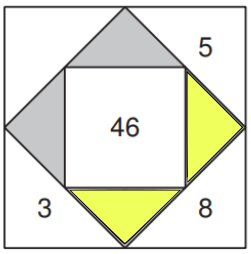
Um auf die Zahl in den Dreiecken zu kommen, muss man den Wert der angrenzenden Dreiecke addieren.
5 + 8 = 13
3 + 8 = 11
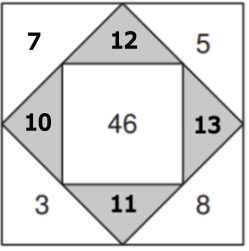
Welche Zahl gehört in das gelb markierte Dreieck?
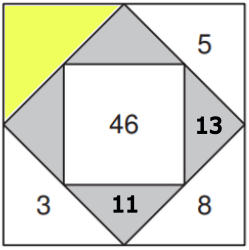
Wenn du die Zahl kennst, kannst du das ganze Rechenquadrat ausfüllen.

Wenn du die Zahl kennst, kannst du das ganze Rechenquadrat ausfüllen.
- 7
- 9
- 6
- 8
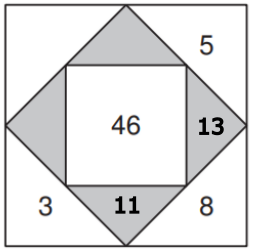
Um auf die Zahl zu kommen:
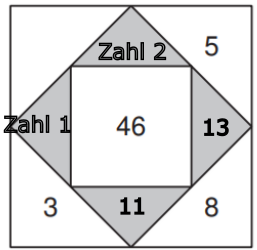
Die Zahl 46 ist die Summe der umliegenden grauen Dreiecke (11 + 13 + Zahl 1 + Zahl 2)
Wir kennen aber nur zwei der grauen Dreiecke. Wie finden wir Zahl 1 und Zahl 2?
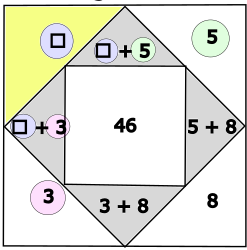
Zahl 1 setzt sich aus der Zahl in der äusseren, gelb markierten Ecke und der Zahl 3 zusammen (☐ + 3).
Zahl 2 setzt sich aus der Zahl in der äusseren, gelb markierten Ecke und der Zahl 5 zusammen (☐ + 5).
Zahl 1 und 2 müssen, wenn man sie zusammenzählt, 22 ergeben (weil 11 + 13 + 22 = 46)
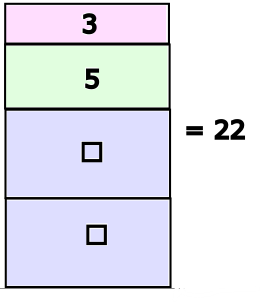
22 - 5 - 3 = 14
14 : 2 = 7
7 ist die Zahl in der äusseren Ecke.
Endresultat
- 11, 13, 12, 10
- 11, 13, 8, 14
- 11, 12, 9, 14
- 12, 15, 9, 10
- 5, 8, 16, 17
- 11, 9, 16, 10
- 12, 14, 11, 10
- 9, 15, 11, 11
b) Ergänze die fehlenden sechs Zahlen im untenstehenden Rechenquadrat so, dass es folgende Eigenschaften hat:
• Die Zahlen in den oberen beiden weissen Dreiecken sind ungerade Zahlen.
• Alle neun Zahlen des Rechenquadrats sind verschieden.
• Die Zahlen in den oberen beiden weissen Dreiecken sind ungerade Zahlen.
• Alle neun Zahlen des Rechenquadrats sind verschieden.

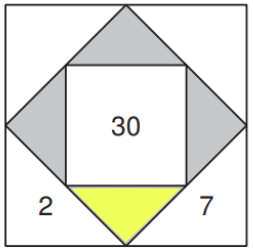
Welche Zahl gehört in das gelb markierte Dreieck?

- 5
- 13
- 11
- 9
Um auf die Zahl in den Dreiecken zu kommen, muss man den Wert der angrenzenden Dreiecke addieren.
2 + 7 = 9
Um die Aufgabe weiterlösen zu können, müssen wir das System hinter den Rechenquadraten kennen.
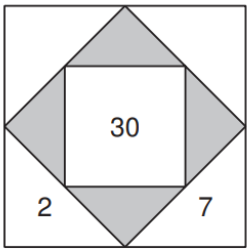
Die folgende Abbildung zeigt ein vollständig ausgefülltes Rechenquadrat (nicht von dieser Aufgabe)
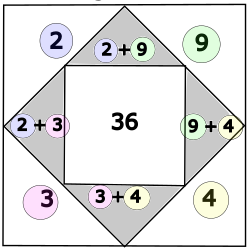
Bilde zuerst die Summe der äussersten Dreiecke und anschliessend die Summe der grauen Dreiecke.
Vervollständige dann den Satz: "Die Summe der grauen Dreiecke ist ... die Summe der äussersten Dreiecke".
Die folgende Abbildung zeigt ein vollständig ausgefülltes Rechenquadrat (nicht von dieser Aufgabe)

Bilde zuerst die Summe der äussersten Dreiecke und anschliessend die Summe der grauen Dreiecke.
Vervollständige dann den Satz: "Die Summe der grauen Dreiecke ist ... die Summe der äussersten Dreiecke".
- halb so gross wie
- doppelt so gross wie
- drei Mal
- vier Mal
Die Summe der grauen Dreiecke ist doppelt so gross wie die Summe der äussersten Dreiecke.
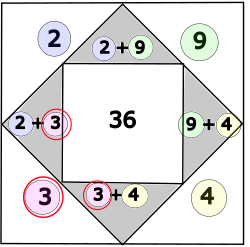
Schau dir als Beispiel die Zahl 3 in den äussersten Dreiecken vor.
In den äussersten Dreiecken kommt sie einmal vor.
In den grauen Dreiecken kommt sie aber zwei Mal (also doppelt so oft) vor, weil sie hier als "Baustein" verwendet wird.
Das gilt für alle Zahlen der äussersten Dreiecke und ist der Grund, weshalb die Summe der grauen Dreiecke das Doppelte der Summe der äussersten Dreiecke ist.
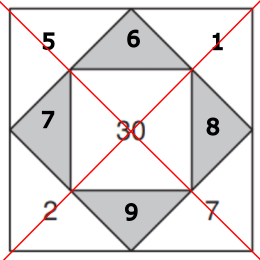
Zurück zu unserer Aufgabe: Wie gross muss die Summe der äussersten Dreiecke sein?
- 30
- 10
- 7
- 15
Summe der grauen Dreiecke: 30
Summe der äussersten Dreiecke 30 : 2 = 15
Begründung: Die Summe der äussersten Dreiecke ist halb so gross wie die der grauen Dreiecke
Welche Zahlen gehören in die gelb markierten Dreiecke?
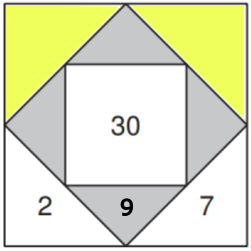

- 1 und 4
- 2 und 4
- 1 und 5
- 3 und 4
Summe der äussersten Dreiecke: 15
15 - 2 - 7 = 6
Die zwei noch unbekannten Zahlen müssen zusammen 6 ergeben.
Da keine zwei Zahlen im Rechenquadrat gleich sein dürfen und alle Zahlen ungerade sein müssen kommen nur die Zahlen 1 und 5 in Frage.
Fülle alle fehlenden Zahlen ins Rechenquadrat ein. Welche Zahlen findest du in den grauen Dreiecken?
- 3, 6, 12, 9
- 7, 6, 12, 9
- 7, 6, 8, 9
- 5, 1, 7, 2
Die Platzierung der Zahlen in den Dreiecken bestimmt die Werte der grauen Dreiecke. Nur die folgende Anordnung kommt in Frage:
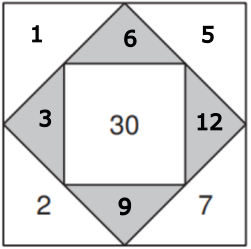
Wenn die 1 und die 5 in den äussersten Dreicken den Platz tauschen würden, würde die Zahl 7 zwei Mal vorkommen, was gegen die Regeln der Aufgabenstellung verstossen würde:
Endresultat
- 7, 6, 12, 9
- 7, 6, 8, 9
- 5, 1, 7, 2
- 3, 6, 12, 9
- 5, 6, 8, 11
- 7, 6, 12, 5
- 13, 6, 8, 3
- 11, 7, 8, 4
