6.
In der Abbildung siehst du das Netz eines Quaders.?
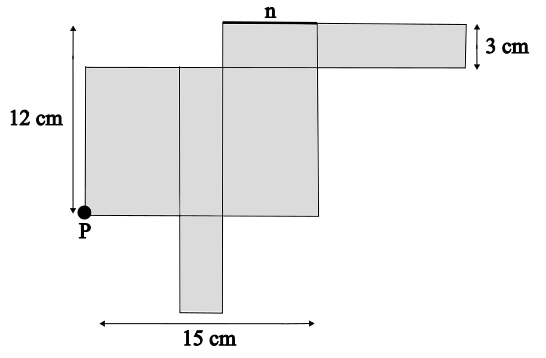
a) Wie viele cm³ beträgt das Volumen des zusammengefalteten Quaders?

a) Wie viele cm³ beträgt das Volumen des zusammengefalteten Quaders?
Volumen eines Quaders = Länge \(\cdot\) Breite \(\cdot\) Höhe
Was ist die Höhe des Quaders?
Was ist die Höhe des Quaders?
- 6 cm
- 5 cm
- 3 cm
- 4 cm
Höhe = 3 cm
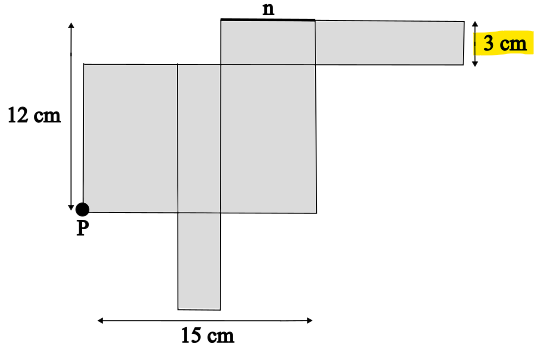
Was ist die Länge des Quaders?
- 18 cm
- 9 cm
- 7 cm
- 30 cm
Länge = 9 cm
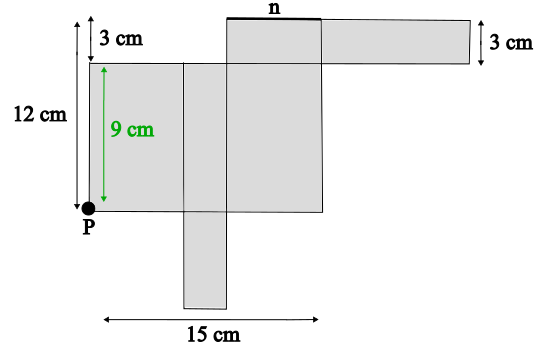
Was ist die Breite des Quaders
- 6 cm
- 5 cm
- 8 cm
- 12 cm
Breite = 6 cm
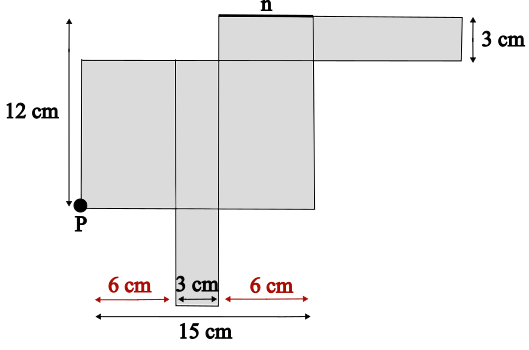
Volumen = Länge \(\cdot\) Breite \(\cdot\) Höhe
Was ist das Volumen des Quaders?
Was ist das Volumen des Quaders?
- 223 cm³
- 230 cm³
- 400 cm³
- 162 cm³
3 cm \(\cdot\) 9 cm \(\cdot\) 6 cm = 162 cm³
Endresultat
- 980 cm³
- 223 cm³
- 230 cm³
- 400 cm³
- 162 cm³
- 420 cm³
- 160 cm³
- 600 cm³
- 800 cm³
b) Die markierte Kante n müsste dabei mit einer anderen Kante verklebt werden. Markiere diese andere Kante deutlich im Netz und beschrifte sie ebenfalls mit n.
Bei welcher Zahl liegt die gesuchte Kante?
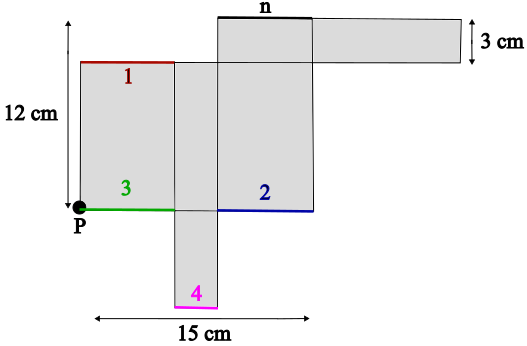
Bei welcher Zahl liegt die gesuchte Kante?

Bei welcher Zahl liegt die gesuchte Kante?


- 2
- 3
- 1
- 4
Die Kante n wird mit der Kante 1 verklebt.
Endresultat
- 1
- 2
- 3
- 4
c) Für die markierte Ecke P im Netz gibt es noch zwei andere Punkte im Netz so, dass
diese Punkte im zusammengefalteten Quader auf die Ecke P fallen. Bei welchen Zahlen liegen die gesuchten Punkte?
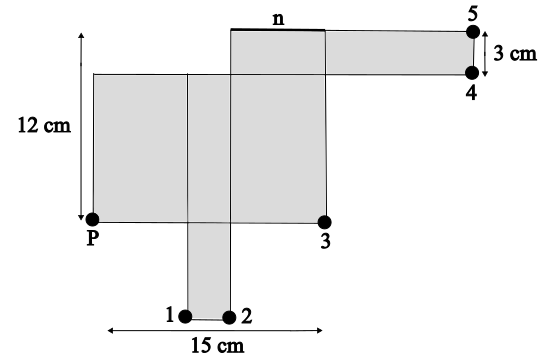

Bei welchen Zahlen liegen die gesuchten Punkte?


- 1 und 3
- 3 und 5
- 1 und 5
- 2 und 3
Die Punkte 1 und 5 werden mit P verklebt
Endresultat
- 1 und 4
- 2 und 4
- 1 und 3
- 3 und 5
- 1 und 5
- 2 und 3
- 1 und 2
- 4 und 5
- 2 und 5
