6.
Laura und Emil haben einen Garten. Da sie beide vier Sorten Gemüse anpflanzen wollen, unterteilen sie den Gaten jeweils in vier rechteckige Beete.
a) Berechne den Umfang von Laras Garten (siehe Figur, nicht massstäblich).
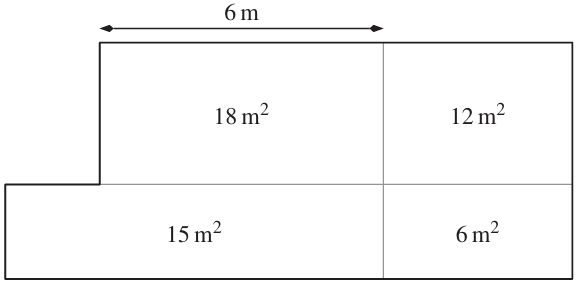
a) Berechne den Umfang von Laras Garten (siehe Figur, nicht massstäblich).

Wie lange ist die gelb markierte Strecke?
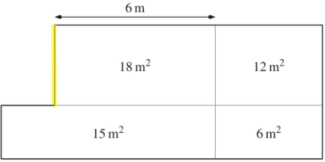

- 2m
- 3m
- 4m
- 6m
Die gelb markierte Strecke ist 3m lang. Die Fläche des Gartenabteils beträgt 18m2.
Die Länge des Gartenabteils beträgt 6m.
Länge \(\cdot\) Breite = Fläche
Fläche : Länge = Breite
Also: 18m2 : 6m = 3m.
Wie lange ist die gelb markierte Strecke?
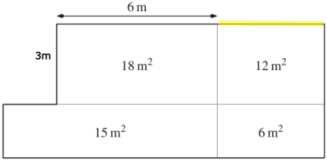

- 2m
- 3m
- 4m
- 6m
Die gelb markierte Strecke ist 4m lang. Die Fläche des Gartenabteils beträgt 12m2.
Die Breite des Gartenabteils beträgt 3m (haben wir im vorherigen Schritt berechnet).
Länge \(\cdot\) Breite = Fläche
Fläche : Breite = Länge
Also: 12m2 : 3m = 4m.
Wie lange ist die gelb markierte Strecke?

- 1m
- 2.5m
- 1.5m
- 0.5m
Die gelb markierte Strecke ist 1.5m lang. Die Fläche des Gartenabteils beträgt 6m2.
Die Länge des Gartenabteils beträgt 4m (haben wir im vorherigen Schritt berechnet).
Länge \(\cdot\) Breite = Fläche
Fläche : Länge = Breite
Also: 6m2 : 4m = 1.5m
Wie lange ist die gelb markierte Strecke?
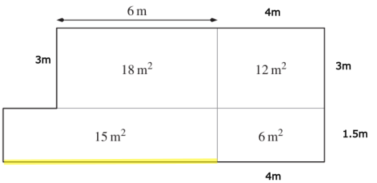

- 12.5m
- 7.5m
- 12m
- 10m
Die gelb markierte Strecke ist 10m lang. Die Fläche des Gartenabteils beträgt 15m2.
Die Breite des Gartenabteils beträgt 1.5m (haben wir im vorherigen Schritt berechnet).
Länge \(\cdot\) Breite = Fläche
Fläche : Breite = Länge
Also: 15m2 : 1.5m = 10m (Tipp: 15 : 1.5 = 50 : 15)
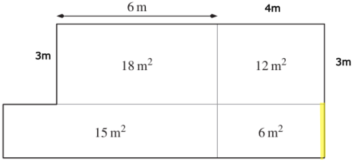
Wie lange ist die gelb markierte Strecke?
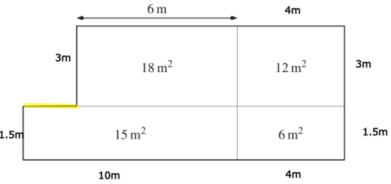

- 4m
- 6m
- 3m
- 1.5m
Die gelb markierte Strecke ist 4m lang.
Länge des unteren linken Gartenabteils - Länge des oberen linken Gartenabteils.
10m - 6m = 4m
Was ist der Umfang des Gartens?
- 37m
- 27m
- 21m
- 23m
Der Umfang des Gartens ist die Länge, die eine Schnur haben würde, wenn du sie einmal um den Garten legen würdest.
Normalerweise würde man einfach alle Seitenlängen zusammenzählen. Hier kannst du es noch einfacher machen, denn die Einbuchtung an der linken Seite des Gartens spielt für den Umfang keine Rolle (mehr dazu in Aufgabe b)
14 \(\cdot\) 2 + 4.5 \(\cdot\) 2 = 37m
Endresultat
- 27m
- 23m
- 61m
- 52m
- 37m
- 63m
- 31m
- 53m
b) Berechne den Umfang von Emils Garten (siehe Figur, nicht massstäblich).
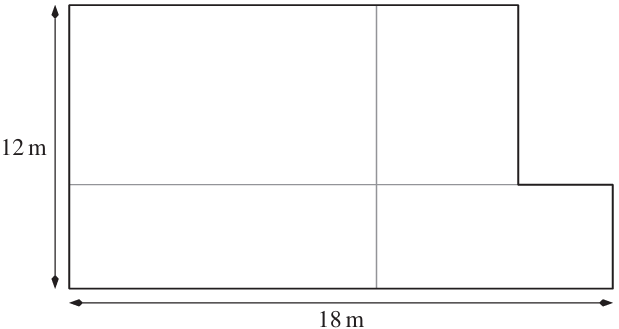

Die Aufgabe ist einfacher, als sie auf den ersten Blick erscheint. Die Einbuchtung an der rechten Breite des Gartens hat einen Einfluss auf seine Fläche, nicht aber seinen Umfang. Was ist der Umfang des Gartens?
- 216m
- 72m
- 60m
- 186m
Der Umfang beträgt 60m
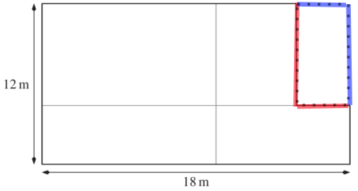
Die Einbuchtung an der rechten Breite des Gartens hat einen Einfluss auf seine Fläche, nicht aber seinen Umfang.
Man kann also einfach Länge + Breite + Länge + Breite rechnen.
18 + 12 + 18 + 12 = 60m Umfang.
Endresultat
- 216m
- 72m
- 50m
- 58m
- 78m
- 102m
- 60m
- 186m
