4.
a) Abgebildet ist ein Punktmuster aus grauen, schwarzen und weissen Punkten.

Welchen Anteil aller Punkte machen
- Die weissen Punkte aus,
- Die grauen Punkte aus,
- Die schwarzen Punkte aus
Gib jeweils den vollständig gekürzten Bruch an.

Welchen Anteil aller Punkte machen
- Die weissen Punkte aus,
- Die grauen Punkte aus,
- Die schwarzen Punkte aus
Gib jeweils den vollständig gekürzten Bruch an.
Wie viele Punkte gibt es insgesamt?
- 16 Punkte
- 12 Punkte
- 20 Punkte
- 15 Punkte
In der Breite sind es 4 Punkte, in der Länge 5 Punkte.
4 \(\cdot\) 5 = 20 Punkte insgesamt.
Was ist der ungekürzte Anteil der weissen Punkte?
- 20/4
- 4/20
- 5/20
- 20/5
Es gibt 4 weisse Punkte und 20 Punkte insgesamt. Der ungekürzte Anteil der weissen Punkte ist also 4/20
Kürze den Bruch 4/20.
Erinnerung: Brüche kürzt man, indem man den Zähler und den Nenner durch die gleiche Zahl teilt. Der Wert des Bruchs bleibt dabei gleich.
Erinnerung: Brüche kürzt man, indem man den Zähler und den Nenner durch die gleiche Zahl teilt. Der Wert des Bruchs bleibt dabei gleich.
- 1/6
- 1/4
- 2/5
- 1/5
Der Zähler (4) und der Nenner (20) sind beide durch 4 teilbar. Der gekürzte Bruch ist also 1/5.
Nun für die grauen Punkte: Was ist der Anteil grauer Punkte, angegeben als gekürzter Bruch?
- 1/2
- 1/5
- 1/20
- 1/10
Es gibt 10 graue Punkte und 20 Punkte insgesamt. Der Anteil der grauen Punkte ist 10/20, gekürzt also 1/2.
Nun für die schwarzen Punkte: Was ist der Anteil schwarzer Punkte, angegeben als gekürzter Bruch?
- 1/6
- 2/5
- 3/10
- 1/10
Es gibt 6 schwarze Punkte und 20 Punkte insgesamt. Der Anteil der schwarzen Punkte ist also 6/20.
Der gekürzte Bruch ist 3/10.
Endresultat
- Weisse: 1/5, Graue: 1/2, Schwarze: 3/10
- Weisse: 1/4, Graue: 1/10, Schwarze: 3/10
- Weisse: 1/5, Graue: 2/5, Schwarze: 1/6
- Weisse: 1/6, Graue: 1/20, Schwarze: 2/5
- Weisse: 1/5, Graue: 1/10, Schwarze: 1/10
b) Im abgebildeten Zahlenstrahl sind die Brüche 1/2 und 3/4 eingezeichnet.
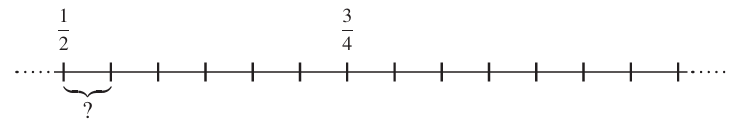
- Wie gross ist der Abstand zwischen zwei benachbarten Strichen?
- Welcher Punkt entspricht auf dem Zahlenstrahl dem Bruch 5/6

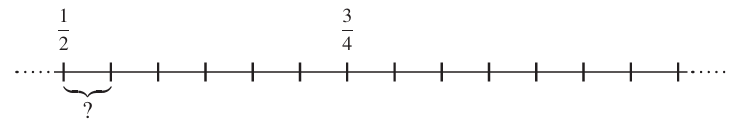
- Wie gross ist der Abstand zwischen zwei benachbarten Strichen?
- Welcher Punkt entspricht auf dem Zahlenstrahl dem Bruch 5/6

Was ist die Differenz zwischen 3/4 und 1/2? Tipp: Die Brüche brauchen denselben Nenner, um das zu berechnen.
- 1/4
- 1/2
- 2/4
- 1/5
Die Differenz ist 1/4.
1/2 kann zu 2/4 erweitert werden, indem man den Zähler und Nenner jeweils mit 2 multipliziert. Der Wert bleibt dadurch gleich.
3/4 - 2/4 = 1/4
Notiz zum Thema Brüche erweitern:
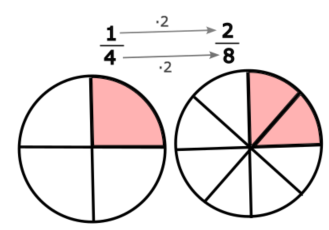
Wie gross ist der Abstand zwischen zwei benachbarten Strichen? Tipp: Indem du die Abstände zählst, weisst du, wie viele Abstände zusammen 1/4 geben.
- 1/12
- 1/16
- 1/10
- 1/24
Der Abstand zwischen zwei benachbarten Strichen ist 1/24.
6 Abstände zusammen ergeben 1/4.

Um zu berechnen wie gross ein Abstand ist, muss 1/4 durch 6 geteilt werden.
Ein Bruch wird geteilt, indem man mit dem Kehrwert des zweiten Bruchs multipliziert.
6 ist dasselbe wie 6/1. Der Kehrwert davon ist 1/6
1/4 : 6/1 = 1/4 \(\cdot\) 1/6
Brüche zu multiplizieren ist einfach: Man multipliziert die beiden Zähler und die beiden Nenner.
1/4 \(\cdot\) 1/6 = 1/24
Nun zum zweiten Teil der Aufgabe: Welchen Bruch mit dem Nenner 24 erhält man, wenn man 5/6 erweitert?
- 22/24
- 20/24
- 15/24
- 18/24
5/6 kann zu 20/24 erweitern.
Für den Nenner weiss man: 6 \(\cdot\) 4 = 24.
Um einen Bruch zu erweitern multipliziert man den Zähler und den Nenner mit der gleichen Zahl. Somit kennt man den Zähler des erweiterten Bruchs: 5 \(\cdot\) 4 = 20.
Welchen Bruch mit dem Nenner 24 erhält man, wenn man 3/4 erweitert?
- 22/24
- 20/24
- 15/24
- 18/24
3/4 kann zu 18/24 erweitern.
Für den Nenner weiss man: 4 \(\cdot\) 6 = 24.
Um einen Bruch zu erweitern multipliziert man den Zähler und den Nenner mit der gleichen Zahl. Somit kennt man den Zähler des erweiterten Bruchs: 3 \(\cdot\) 6 = 18.
Welcher Punkt entspricht auf dem Zahlenstrahl dem Bruch 5/6 (beziehungsweise 20/24)


- 1
- 2
- 3
- 4
Der Punkt entspricht Punkt 3.
3/4 = 18/24
5/6 = 20/24
Da der Abstand von einem Strich zum nächsten 1/24 beträgt und zwei Abstände zwischen 18/24 und 20/24 liegen, muss 5/6 bei Punkt 3 liegen.
Endresultat
- Der Abstand ist 1/12, 5/6 ist bei Punkt 3
- Der Abstand ist 1/10, 5/6 ist bei Punkt 2
- Der Abstand ist 1/24, 5/6 ist bei Punkt 3
- Der Abstand ist 1/20, 5/6 ist bei Punkt 1
- Der Abstand ist 1/16, 5/6 ist bei Punkt 4
- Der Abstand ist 1/24, 5/6 ist bei Punkt 2
- Der Abstand ist 1/16, 5/6 ist bei Punkt 3
- Der Abstand ist 1/16, 5/6 ist bei Punkt 4
