2.
a) Welche Punkte im Koordinatensystem entsprechen den unten genannten Punkten A, B und C?
A(5/2), B(7/5), C(4/4)
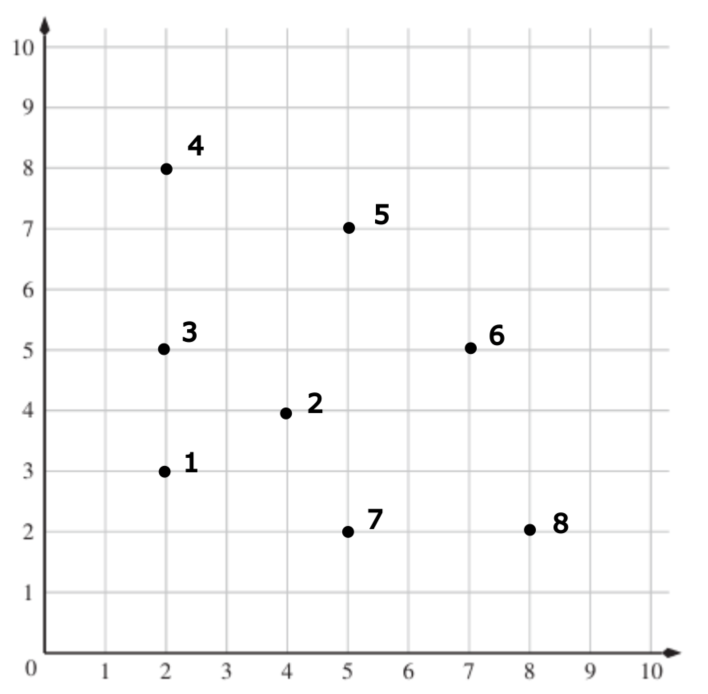
A(5/2), B(7/5), C(4/4)

Welcher der folgenden Punkte entspricht Punkt A?
- 1
- 4
- 7
- 6
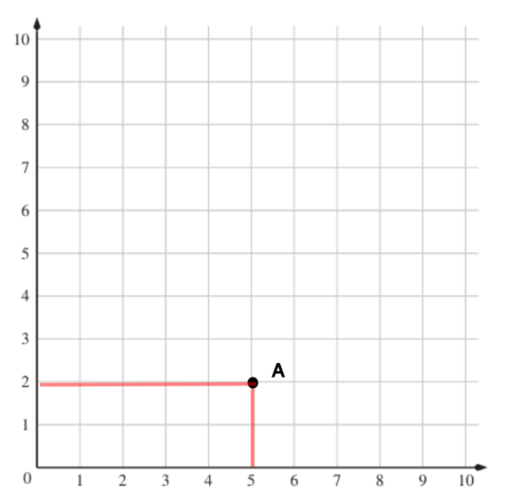
Für A(5/2): Die erste Zahl (5) bezieht sich auf die x-Achse (die waagrechte Achse). Die zweite Zahl (2) bezieht sich auf die y-Achse (die senkrechte Achse).
Welcher der folgenden Punkte entspricht Punkt B?
- 1
- 2
- 6
- 4
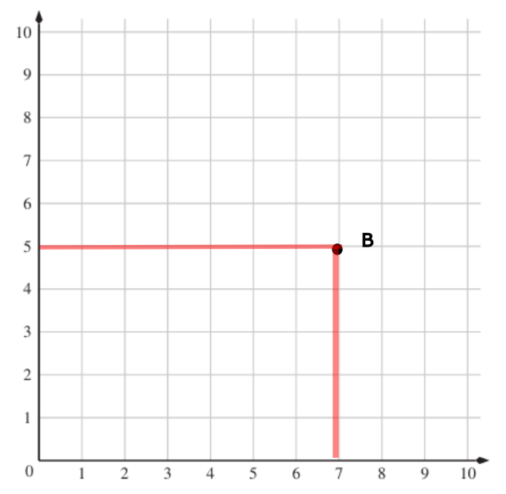
Für B(7/5): Die erste Zahl (7) bezieht sich auf die x-Achse (die waagrechte Achse). Die zweite Zahl (5) bezieht sich auf die y-Achse (die senkrechte Achse).
Welcher der folgenden Punkte entspricht Punkt C?
- 1
- 2
- 3
- 4
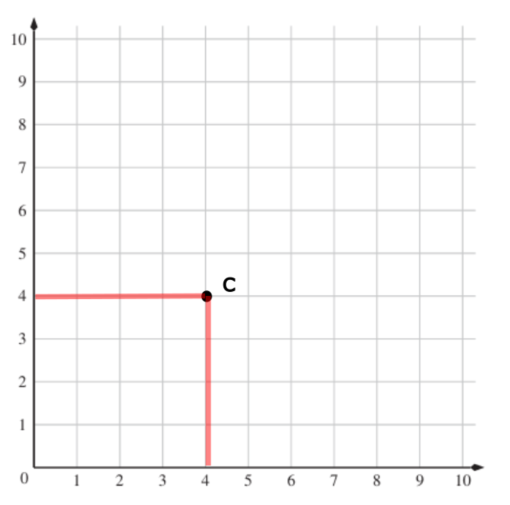
Für C(4/4): Die erste Zahl (4) bezieht sich auf die x-Achse (die waagrechte Achse). Die zweite Zahl (4) bezieht sich auf die y-Achse (die senkrechte Achse).
Endresultat
- A=4, B=6, C=8
- A=3, B=5, C=2
- A=7, B=6, C=2
- A=4, B=5, C=2
- A=3, B=6, C=1
- A=1, B=7, C=3
- A=3, B=6, C=2
- A=1, B=5, C=6
- A=3, B=5, C=8
b) Es gibt mehrere Möglichkeiten, das Dreieck ABC mit einem vierten Punkt zu einem Parallelogramm zu ergänzen.
Welche Punkte sind möglich? Tipp: Zeichne das Dreieck aus Aufgabe a) auf und überlege dann weiter.
Was macht ein Parallelogram aus? Wähle die genauste Beschreibung.
- Viereck wo alle Seiten parallel sind.
- Viereck mit zwei parallelen, gleich langen Seiten.
- Viereck mit zwei parallen, ungleich langen Seiten.
- Es ist eine Art von Rechteck.
Ein Parallelogram ist ein Viereck mit zwei parallelen, gleich langen Seiten.
Nennen wir den vierten Punkt P. Wo wäre P, wenn P zwischen Punkten A und C liegen würde? Erinnerung: Die Seite CP muss gleich lang sein wie die Seite AB des Dreiecks.
- (3/2)
- (3/3)
- (2/2)
- (2/1)
Der Punkt P wäre (2/1).
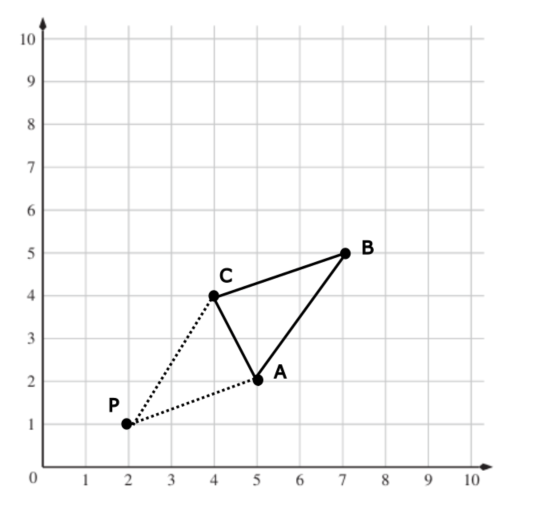
Nennen wir den vierten Punkt P. Wo wäre P, wenn P zwischen Punkten C und B liegen würde? Erinnerung: Die Seite CP muss gleich lang sein wie die Seite AB des Dreiecks.
- (5/6)
- (5/5)
- (6/7)
- (7/7)
Der Punkt P wäre (6/7).
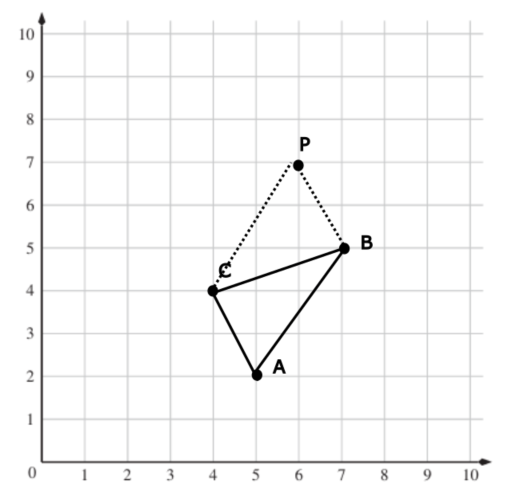
Nennen wir den vierten Punkt P. Wo wäre P, wenn P zwischen Punkten A und B liegen würde? Erinnerung: Die Seite BP muss gleich lang sein wie die Seite AC des Dreiecks.
- (8/3)
- (8/4)
- (7/4)
- (7/3)
Der Punkt P wäre (6/7).
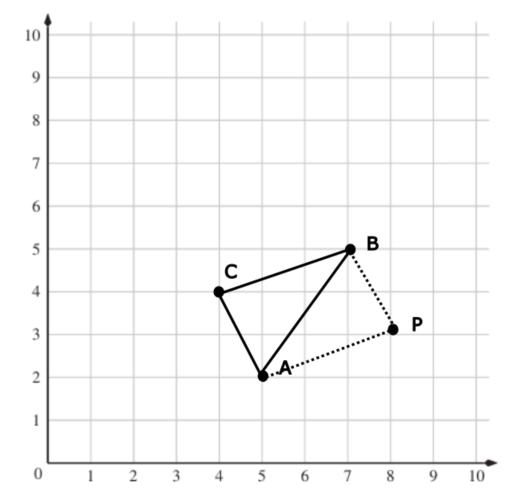
Endresultat
- Folgende Punkte sind möglich: (3/2), (6/6), (8/4)
- Folgende Punkte sind möglich: (2/1), (6/7), (8/4)
- Folgende Punkte sind möglich: (2/2), (6/7), (8/3)
- Folgende Punkte sind möglich: (2/1), (6/7), (8/3)
- Folgende Punkte sind möglich: (2/2), (5/6), (8/4)
