3.
Die untenstehende Burg ist aus Würfeln von 1 cm
Kantenlänge zusammengeklebt. Sie ist auf einem Sockel gebaut und sieht von allen Seiten gleich aus. Der Sockel hat keinen Hohlraum.
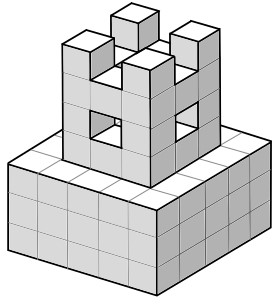
a) Aus wie vielen Würfeln besteht die Burg?

a) Aus wie vielen Würfeln besteht die Burg?
Wenn du dir die Wände der Burg anschaust, siehst du, dass sie aus verschiedenen Elementen aufgebaut ist:
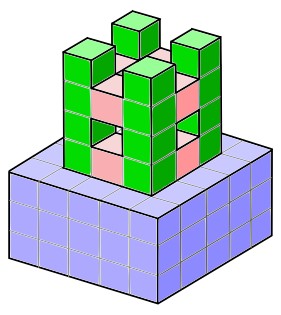
Der untere Teil Burg besteht aus einem Sockel (blau).
Der obere Teil der Burg besteht aus vier Ecken (grün) und vier Wänden mit Löchern (rot)
Berechne zuerst, wie viele Würfel im Sockel der Burg enthalten sind.

Der untere Teil Burg besteht aus einem Sockel (blau).
Der obere Teil der Burg besteht aus vier Ecken (grün) und vier Wänden mit Löchern (rot)
Berechne zuerst, wie viele Würfel im Sockel der Burg enthalten sind.
- 65 Würfel
- 95 Würfel
- 80 Würfel
- 75 Würfel
Der Sockel ist 5 Würfel lang, 5 Würfel breit und 3 Würfel hoch.
Er besteht also aus: 5 \(\cdot\) 5 \(\cdot\) 3 = 75 Würfel
Berechne als nächstes wie viele Würfel in den Ecken (grün) im oberen Teil der Burg enthalten sind.
- 16 Würfel
- 20 Würfel
- 24 Würfel
- 22 Würfel
Jede Ecke im oberen Teil der Burg besteht aus 4 Würfeln
Der obere Teil der Burg hat 4 Ecken.
Insgesamt gibt es also 4 \(\cdot\) 4 = 16 Würfel in den Ecken des oberen Teils der Burg.
Berechne als nächstes die Anzahl Würfel in den Wänden mit Löchern (rot) im oberen Teil der Burg.
- 12 Würfel
- 5 Würfel
- 10 Würfel
- 8 Würfel
Die vier Wände mit Löcher sehen alle gleich aus (das ist in der Aufgabenstellung gegeben).
Jede dieser Wände besteht aus 2 Würfeln.
Es gibt 4 Wände mit Löchern
In den Wänden mit Löchern sind also insgesamt 2 \(\cdot\) 4 = 8 Würfel enthalten
Zähle die Würfel der Ecken und Wänden zusammen. Wie viele Würfel erhältst du?
- 72 Würfel
- 99 Würfel
- 106 Würfel
- 110 Würfel
75 + 16 + 8 = 99 Würfel
Endresultat
- 72 Würfel
- 99 Würfel
- 106 Würfel
- 110 Würfel
- 69 Würfel
- 95 Würfel
- 100 Würfel
- 123 Würfel
b) Wie viele Würfel der Burg berühren den Boden?
Die gesamte Unterseite des Sockels berührt den Boden. Wie viele Würfel sind das?
- 35 Würfel
- 15 Würfel
- 30 Würfel
- 25 Würfel
Der Sockel ist 5 Würfel lang und 5 Würfel breit.
Somit berühren 5 \(\cdot\) 5 = 25 Würfel den Boden
Endresultat
- 21 Würfel
- 35 Würfel
- 15 Würfel
- 30 Würfel
- 25 Würfel
- 20 Würfel
- 40 Würfel
- 10 Würfel
c) Wie viele Würfel braucht es zusätzlich, um aus der Burg einen vollständig gefüllten Quader mit 5 cm Länge, 5 cm Breite und 7 cm Höhe zu erhalten?
Der Sockel ist bereits gefüllt. Schau dir also nur den oberen Teil der Burg an. Wie viele Würfel werden gebraucht, um die Hohlräume des oberen Burgteils zu füllen?
- 17 Würfel
- 16 Würfel
- 12 Würfel
- 14 Würfel
Um die Löcher in den Wänden zu füllen, werden 8 Würfel gebraucht. Um den Innenraum des oberen Burgteils zu füllen werden 4 Würfel gebraucht.
Um die Hohlräume des oberen Burgteils zu füllen braucht es also 8 + 4 = 12 Würfel
Überlege nun, wie viele Würfel gebraucht werden, um die "Hülle" des oberen Burgteils zu ergänzen, damit ein Quader entsteht.
- 75 Würfel
- 46 Würfel
- 55 Würfel
- 64 Würfel
Damit der geforderte Quader entsteht, muss eine zusätzliche "Schicht" um die Wände des oberen Burgteils gelegt werden.
Diese Schicht besteht aus 64 Würfeln (16 Würfel in den Ecken und 12 Würfel pro Wand)
Addiere die Würfel, die man für das Füllen der Burgwände gebraucht hat zu den Würfeln im Innern der Burg.
- 78 Würfel
- 76 Würfel
- 87 Würfel
- 68 Würfel
64 + 12 = 76 Würfel
Endresultat
- 40 Würfel
- 78 Würfel
- 76 Würfel
- 87 Würfel
- 68 Würfel
- 55 Würfel
- 60 Würfel
- 56 Würfel
