6.
a) Auf dem Zahlenstrahl sind zwei Zahlen A und B markiert.
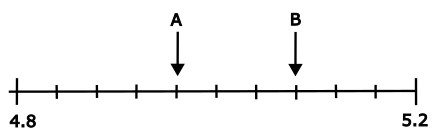
Bestimme A und B. Welche Zahl liegt genau in der Mitte von A und B? Schreibe die drei gesuchten Zahlen auf. Zeige deinen Lösungsweg graphisch oder mit einer Rechnung

Bestimme A und B. Welche Zahl liegt genau in der Mitte von A und B? Schreibe die drei gesuchten Zahlen auf. Zeige deinen Lösungsweg graphisch oder mit einer Rechnung
Wie gross sind die Abstände zwischen den einzelnen Strichen?
- 0.4
- 0.04
- 0.5
- 0.01
Der Zahlenstrahl geht von 4.8 bis 5.2.
Zwischen diesen zwei Zahlen liegen 9 Striche und somit 10 Abstände (das kannst du nachzählen).
Da alle Abstände gleich gross sind, muss man, um von einem kleinen Strich zum nächsten zu kommen, jeweils +0.04 rechnen.
Wenn man das 10 Mal wiederholt (Anzahl Abstände), kommt man von 4.8 (Anfang des Zahlenstrahls) auf 5.2 (Ende des Zahlenstrahls).
Welche Zahl ist A?
- 5.06
- 4.84
- 5
- 4.96
Zwischen 4.8 und A liegen 4 Abstände. Du hast vorher herausgefunden, dass ein Abstand 0.04 gross ist.
A ist also dasselbe wie 4.8 + \((4\cdot0.04)\) = 4.96
Welche Zahl ist B?
- 5.08
- 5.16
- 4.96
- 5
Zwischen 4.8 und B liegen 7 Abstände. Du hast vorher herausgefunden, dass ein Abstand 0.04 gross ist.
B ist also dasselbe wie 4.8 + \((7\cdot0.04)\) = 5.08
Du hast bereits herausgefunden, dass:
A = 4.96
B = 5.08
Jetzt ist die Frage: Welche Zahl liegt in der Mitte zwischen A und B?
A = 4.96
B = 5.08
Jetzt ist die Frage: Welche Zahl liegt in der Mitte zwischen A und B?
- 5.02
- 5
- 4.99
- 5.06
Die Differenz zwischen B und A beträgt 5.08 - 4.96 = 0.12.
Um auf die gesuchte Zahl zu kommen, kann die Hälfte von 0.12 zu A dazugezählt werden.
Die Hälfte von 0.12 ist 0.06.
Es ergibt sich also folgende Rechnung:
4.96 + 0.06 = 5.02
Endresultat
- 5.965
- 5.025
- 5.02
- 5
- 4.99
- 5.06
- 4.99
- 5.6
b)

Welche Zahl liegt zwei Mal so weit von C entfernt wie von D? Zeige deinen Lösungsweg graphisch oder mit einer Rechnung.

Welche Zahl liegt zwei Mal so weit von C entfernt wie von D? Zeige deinen Lösungsweg graphisch oder mit einer Rechnung.
Wie gross ist die Differenz zwischen 2.9 und 3.2?
- 0.2
- 1.2
- 1.3
- 0.3
3.2 - 2.9 = 0.3
Bei welchem Buchstaben müsste die gesuchte Zahl ungefähr liegen?




- A
- F
- E
- D
Die gesuchte Zahl ist von C zweimal weiter entfernt als von D (das steht in der Aufgabenstellung).
Der Abstand der gesuchten Zahl zu D beträgt darum 1/3 des Abstandes zwischen C und D. Das entspricht dem Buchstaben F
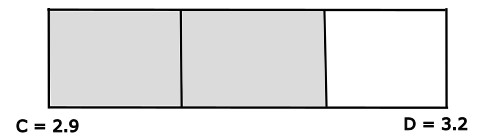
Wie weit ist die gesuchte Zahl von C entfernt?
- 0.1
- 0.2
- 0.02
- 0.3
Der Abstand von C zur gesuchten Zahl beträgt 2/3 der Gesamtstrecke. Die Gesamtstrecke, also den Abstand zwischen 2.9 und 3.2 hast du bereits ausgerechnet.
Für die Distanz von C zur gesuchten Zahl rechnen wir also:
0.3 : 3 = 0.1 (Ein Drittel der Gesamtsrecke)
\(2\cdot0.1\) = 0.2 (Der Abstand zwischen C und der gesuchten Zahl)
Was ist die gesuchte Zahl?
- 3.05
- 2.91
- 3.03
- 3.1
Du rechnest:
2.9 + 0.2 = 3.1
Endresultat
- 2.3
- 2.4
- 2
- 3
- 3.05
- 2.91
- 3.03
- 3.1
