7.
Anna und Fritz bringen zu einer Geburtstagsparty je ein Paket vorbei, das wie in der Skizze mit einer Schnur gebunden ist.
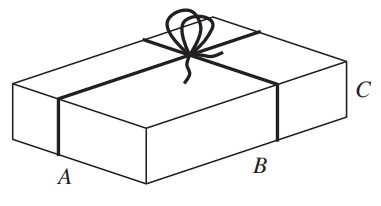
a) Bei Annas Paket ist A = 11 cm, B = 9.5 cm und C = 5.5 cm. Das Paket wurde mit einer 84 cm langen Schnur gebunden. Wie viele Zentimeter der Schnur blieben für die Masche übrig?

a) Bei Annas Paket ist A = 11 cm, B = 9.5 cm und C = 5.5 cm. Das Paket wurde mit einer 84 cm langen Schnur gebunden. Wie viele Zentimeter der Schnur blieben für die Masche übrig?
Von der Schnur, die um das Paket gewickelt ist, haben vier Abschnitte die Länge C:
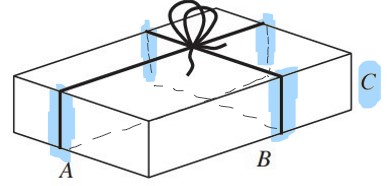
Wie lang sind diese vier Abschnitte zusammen?

Wie lang sind diese vier Abschnitte zusammen?
- 22 cm
- 18 cm
- 15 cm
- 11 cm
C = 5.5 cm
\(4\cdot5.5\) cm = 22 cm
Addiere alle Schnur-Abschnitte mit Länge B.
- 9.5 cm
- 38 cm
- 19 cm
- 27 cm
Die Schnur wird zwei Mal um eine Seite mit der Länge B gelegt.
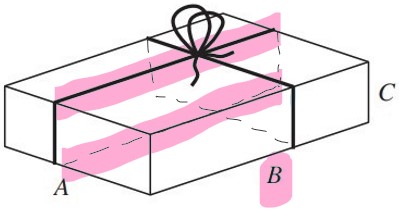
B = 9.5
\(2\cdot9.5\) = 19 cm
Addiere alle Schnur-Abschnitte mit Länge A.
- 11 cm
- 44 cm
- 20 cm
- 22 cm
Die Schnur wird zwei Mal um eine Seite mit der Länge A gelegt.
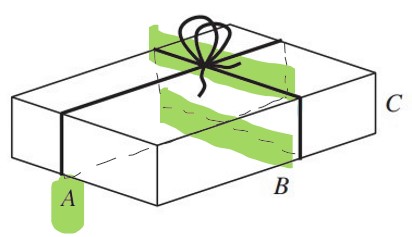
A = 11 cm
\(2\cdot11\) = 22 cm
Wie viel Schnur wird gebraucht, um das Paket zu verpacken (ohne Schleife)?
- 67 cm
- 63 cm
- 76 cm
- 55 cm
22 cm + 19 cm + 22 cm = 63 cm
Wie viel Schnur bleibt für die Schleife übrig?
- 19 cm
- 12 cm
- 21 cm
- 46 cm
84 cm - 63 cm = 21 cm
Endresultat
- 33 cm
- 9 cm
- 10 cm
- 35 cm
- 19 cm
- 12 cm
- 21 cm
- 46 cm
b) Bei Fritz' Paket ist A = 18 cm und B = 15 cm und das Paket hat ein Volumen von 0.54 dm³.
Wie lang ist C?
Berechne das Volumen des Geschenks in cm³
- 5.4 cm³
- 54 cm³
- 540 cm³
- 5400 cm³
Die Umrechnung von dm zu cm funktioniert im Allgemeinen so:
1 dm = 10 cm
1 dm² = 100 cm²
1 dm³ = 1000 cm³
Das bringt uns auf das folgende Resultat:
5.4 dm³ = 540 cm³
Wenn das für dich keinen Sinn ergibt, schau dir die folgende Skizze an:
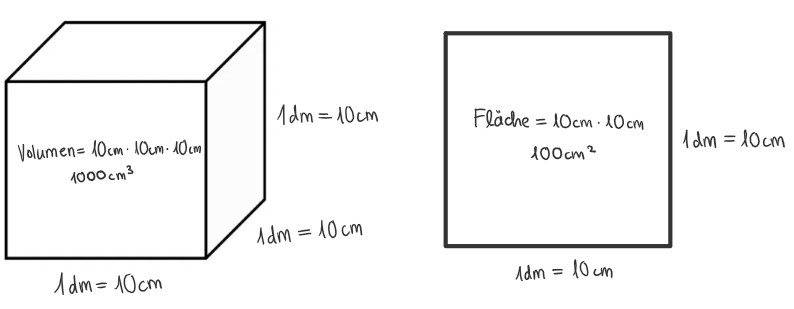
Das Volumen eines Quaders:
Länge \(\cdot\) Breite \(\cdot\) Höhe = Volumen
Wie lang ist C?
Länge \(\cdot\) Breite \(\cdot\) Höhe = Volumen
Wie lang ist C?
- 6 cm
- 5 cm
- 4 cm
- 2 cm
Man muss rückwärtsrechnen, also das Volumen geteilt durch die bekannten Seitenlängen.
540 : 18 = 30
30 : 15 = 2
Die Seite C ist 2 cm lang
Endresultat
- 32 cm
- 2 cm
- 6 cm
- 5 cm
- 7 cm
- 4 cm
- 22 cm
- 12 cm
