7.
Auf dem Frachtschiff "Seahorse" werden zwei Container verladen, die wie in der Skizze mit einer Kette umwickelt sind.
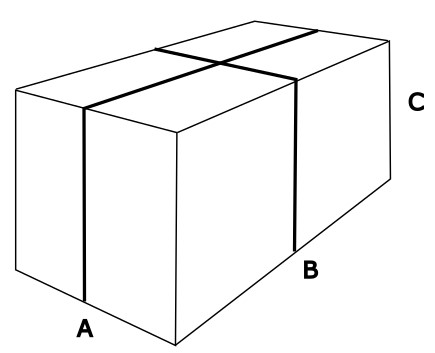
a) Beim ersten Container ist A = 2.5 m, B = 4 m und C = 2 m. Um den Container sicher zu verschliessen, soll er mit der Kette zweimal umwickelt werden. Wie lang muss die Kette mindestens sein?

a) Beim ersten Container ist A = 2.5 m, B = 4 m und C = 2 m. Um den Container sicher zu verschliessen, soll er mit der Kette zweimal umwickelt werden. Wie lang muss die Kette mindestens sein?
Von der Kette, die um den Container gewickelt ist, haben vier Abschnitte die Länge C (wenn der Container einmal umwickelt wird):
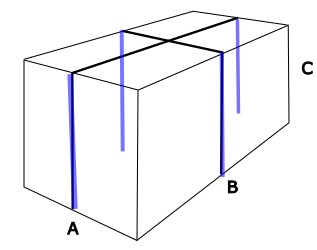
Wie lang sind diese vier Abschnitte zusammen?

Wie lang sind diese vier Abschnitte zusammen?
- 4 m
- 6 m
- 8 m
- 2 m
C = 2 m
\(4\cdot2\) m = 8 m
Addiere alle Ketten-Abschnitte mit Länge B. Gehe für den Anfang davon aus, dass der Container nur einaml umwickelt wird.
- 16 m
- 4 m
- 12 m
- 8 m
Die Kette wird zwei Mal um eine Seite mit der Länge B gelegt.
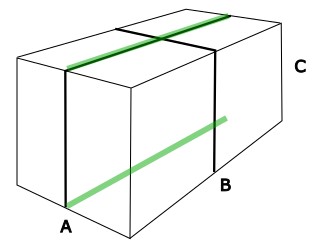
B = 4 m
\(2\cdot4\) = 8 m
Addiere alle Ketten-Abschnitte mit Länge A. Gehe für den Anfang davon aus, dass der Container nur einaml umwickelt wird.
- 5 m
- 4 m
- 2 m
- 6 m
Die Kette wird zwei Mal um eine Seite mit der Länge A gelegt.
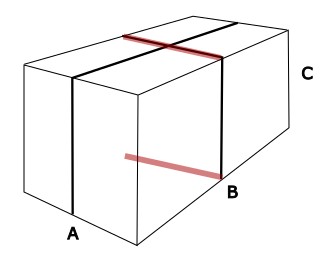
A = 2.5 m
\(2\cdot2.5\) = 5 m
Wie viel Kette wird gebraucht, um den Container einmal zu umwickeln?
- 21 m
- 34 m
- 18 m
- 27 m
8 m + 8 m + 5 m = 21 m
Wie lang muss die Kette sein, um den Container zweimal zu umwickeln?
- 56 m
- 66 m
- 35 m
- 42 m
2 \(\cdot\) 21 = 42 m
Endresultat
- 10.5 m
- 28 m
- 90 m
- 39 m
- 56 m
- 66 m
- 35 m
- 42 m
b) Im Container ist eine Kiste mit Länge = 60 cm und Breite = 25 cm und einem Volumen von 21 dm³ enthalten. Wie hoch ist die Kiste?
Berechne das Volumen des Containers in cm³
- 21 cm³
- 210 cm³
- 2100 cm³
- 21000 cm³
Die Umrechnung von dm zu cm funktioniert im Allgemeinen so:
1 dm = 10 cm
1 dm² = 100 cm²
1 dm³ = 1000 cm³
Das bringt uns auf das folgende Resultat:
21 dm³ = 21000 cm³
Wenn das für dich keinen Sinn ergibt, schau dir die folgende Skizze an:
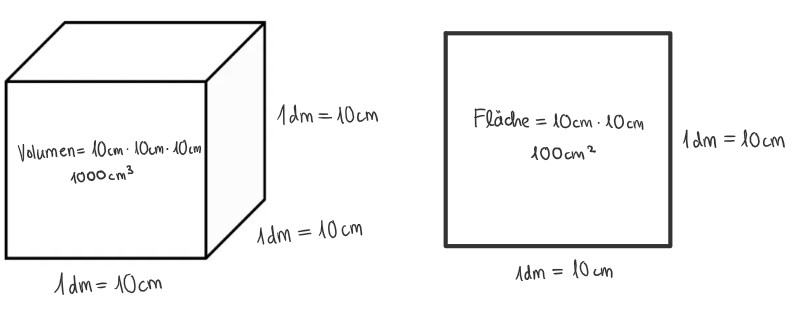
Das Volumen eines Quaders:
Länge \(\cdot\) Breite \(\cdot\) Höhe = Volumen
Wie lang ist C?
Länge \(\cdot\) Breite \(\cdot\) Höhe = Volumen
Wie lang ist C?
- 16 cm
- 14 cm
- 12 cm
- 18 cm
Man muss rückwärtsrechnen, also das Volumen geteilt durch die bekannten Seitenlängen.
21000 : 60 = 350
350 : 25 = 14
Die Seite C ist 14 cm lang
Endresultat
- 16 cm
- 14 cm
- 12 cm
- 18 cm
- 7 cm
- 4 cm
- 22 cm
- 25 cm
