7.
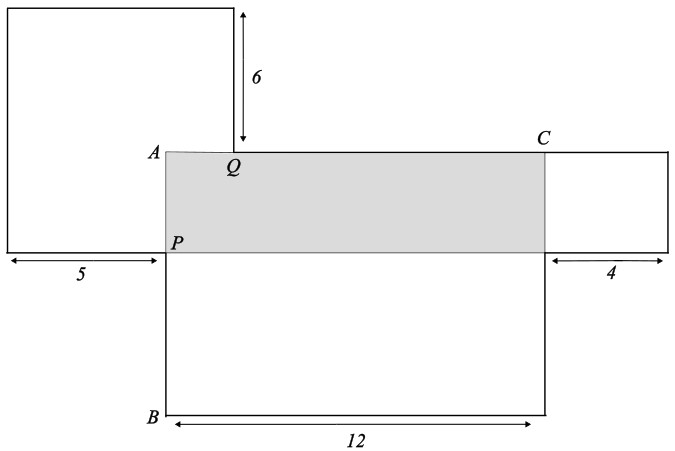
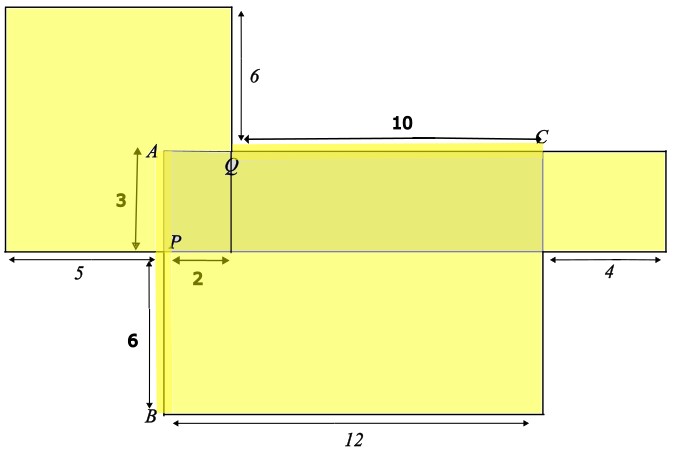
Die folgende Figur (nicht massstäblich) ist aus Rechtecken zusammengesetzt.
Der Abstand zwischen den Punkten P und B ist doppelt so gross wie der Abstand zwischen den Punkten P und A.
Die Strecke QC ist fünfmal grösser als die Strecke AQ.
Der schattierte Teil hat die Fläche 36 cm².
Bestimme die Fläche der gesamten Figur (fett ausgezogen).
Die Strecke QC ist fünfmal grösser als die Strecke AQ.
Der schattierte Teil hat die Fläche 36 cm².
Bestimme die Fläche der gesamten Figur (fett ausgezogen).

Diese Art von Aufgabe ist wie ein Puzzle: Jede zusätzliche Information hilft dir, weiter voranzukommen
Wie lange ist die markierte Strecke?
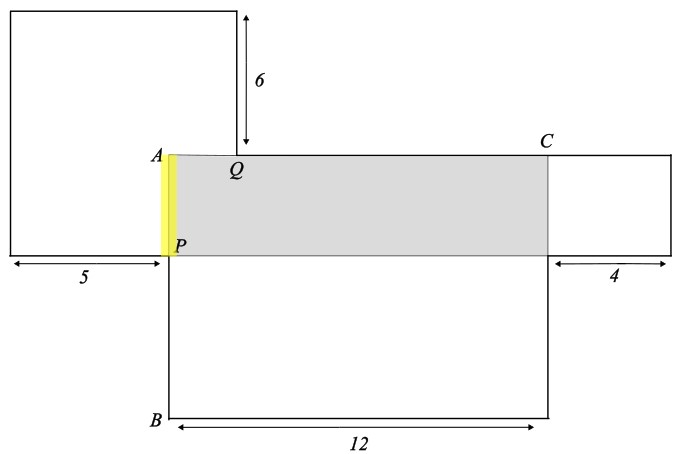
Wie lange ist die markierte Strecke?

- 4 cm
- 3 cm
- 5 cm
- 8 cm
Der Flächeninhalt des schraffierten Rechtecks beträgt 36 cm².
Seine Länge ist in der Abbildung gegeben und beträgt 12 cm.
Seine Breite muss also 36 cm² : 12 cm = 3 cm
Wie lang ist die gelb markierte Strecken?
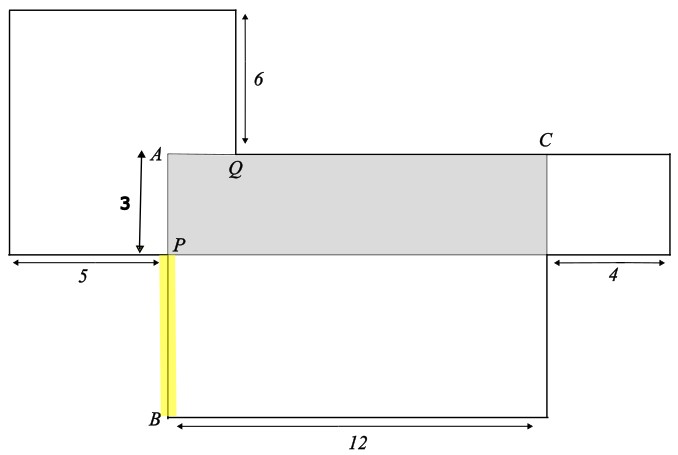

- 3 cm
- 4 cm
- 7 cm
- 6 cm
Der Abstand zwischen den Punkten P und B ist doppelt so gross wie der Abstand zwischen den Punkten P und A.
Somit ist die Strecke AP halb so gross wie die Strecke PB
Die gesuchte Streckenlänge beträgt 3 \(\cdot\) 2 = 6 cm.
Wie lang ist die markierte Strecke?
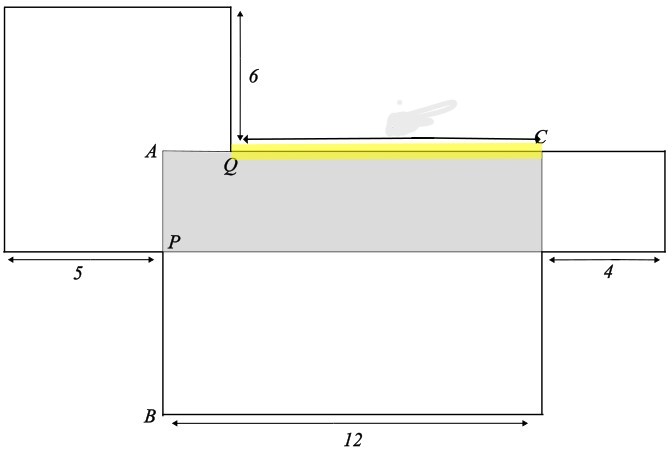

- 12 cm
- 10 cm
- 11 cm
- 8 cm
Die Strecke QC ist fünfmal grösser als die Strecke AQ.
Die Länge der Strecke AC beträgt 12 cm.
Länge AQ = 1/6 von 12
Länge QC = 5/6 von 12
Länge der markierten Strecke = 10 cm
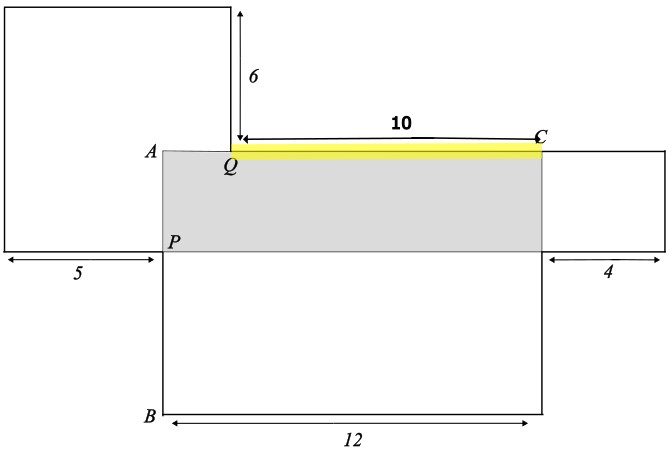
Berechne die Fläche des markierten Rechtecks.

- 42 cm²
- 56 cm²
- 70 cm²
- 68 cm²
Länge des Rechtecks: 14 cm
Breite des Rechtecks: 3 cm
Flächeninhalt = 14 \(\cdot\) 3 = 42 cm²
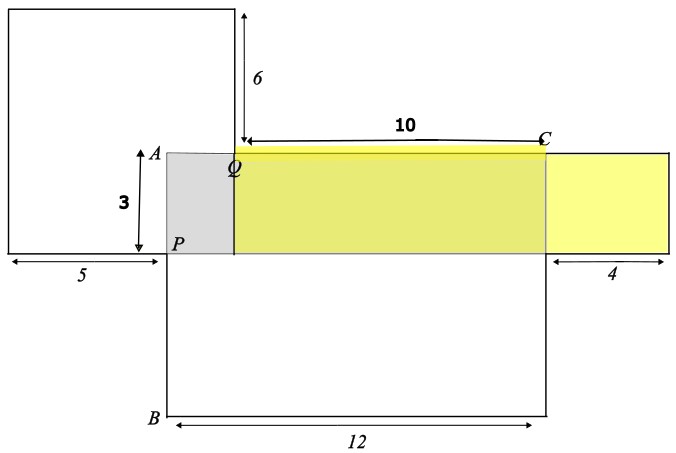
Berechne die Fläche des markierten Rechtecks.

- 99 cm²
- 63 cm²
- 72 cm²
- 54 cm²
Die Länge des Rechtecks beträgt 6 cm + 3 cm = 9 cm.
Die Breite des Rechtecks beträgt 5 cm + 2 cm = 7 cm
Der Flächeninhalt beträgt 9 cm \(\cdot\) 3 cm = 63 cm²
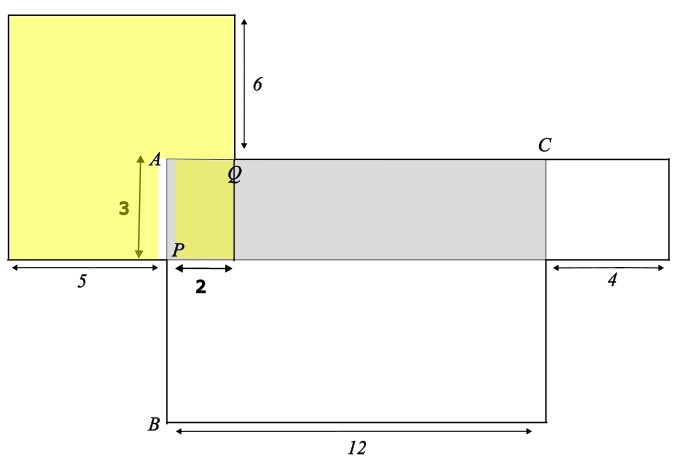
Berechne die Fläche des markierten Rechtecks.

- 106 cm²
- 82 cm²
- 86 cm²
- 72 cm²
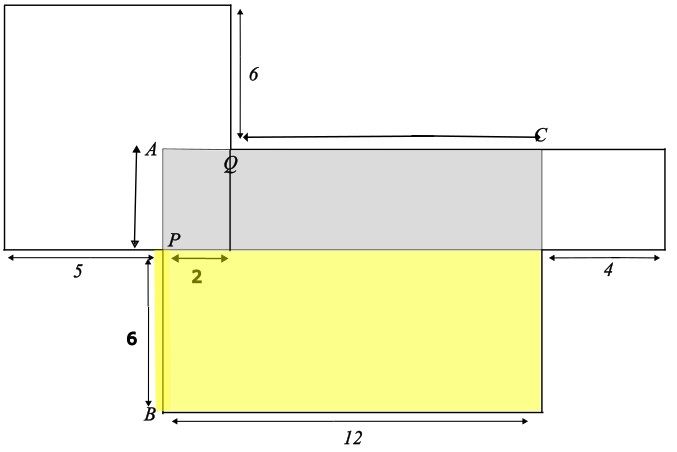
Die Länge des Rechtecks beträgt 12 cm.
Die Breite des Rechtecks beträgt 6 cm
Der Flächeninhalt beträgt 12 cm \(\cdot\) 6 cm = 72 cm²
Berechne die Fläche der gesamten Figur.

- 205 cm²
- 195 cm²
- 183 cm²
- 198 cm²
Flächeninhalt der gesamten Figur: 42 cm² + 63 cm² + 72 cm² = 195 cm²
Endresultat
- 99 cm²
- 107 cm²
- 153 cm²
- 205 cm²
- 195 cm²
- 183 cm²
- 198 cm²
- 232 cm²
