9.
In der Abbildung überschneiden sich ein Quadrat und ein Rechteck in einem rechteckigen Gebiet (in der Abbildung grau),
sodass drei Teilfiguren entstehen. Die drei Teilfiguren haben alle denselben Flächeninhalt.
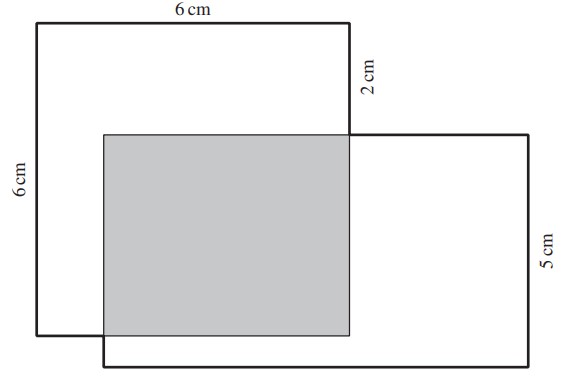
a) Bestimme den Flächeninhalt des grauen Rechtecks.

a) Bestimme den Flächeninhalt des grauen Rechtecks.
Die drei Teilfiguren sind in der folgenden Abbildung eingefärbt. Sie haben alle denselben Flächeninhalt.
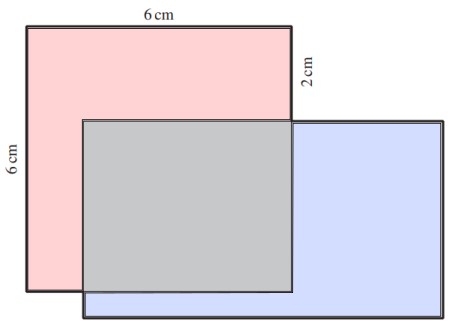
Was ist der Flächeninhalt des grauen Rechtecks?

Was ist der Flächeninhalt des grauen Rechtecks?
- 16 cm²
- 9 cm²
- 14 cm²
- 18 cm²
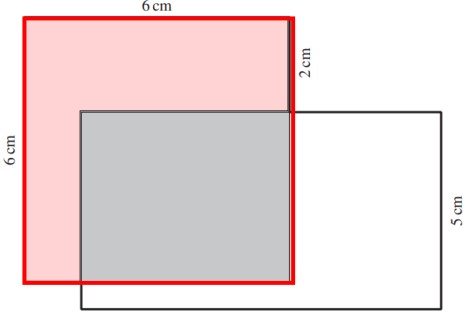
Das rot umrandete Quadrat hat eine Seitenlänge von 6 cm und einen Flächeninhalt von 6 \(\cdot\) 6 = 36 cm²
Das graue Rechteck und das rosa farbene Rechteck haben denselben Flächeninhalt.
Wenn man den Flächeninhalt des grauen Rechtecks und des rosa farbenen Rechtecks addiert, erhält man 36 cm² (den Flächeninhalt des rot umrandeten Rechtecks).
Um den Flächeninhalt des grauen Rechtecks zu berechnen: 36 cm² : 2 = 18 cm²
Endresultat
- 11 cm²
- 16 cm²
- 9 cm²
- 14 cm²
- 18 cm²
- 12 cm²
- 20 cm²
- 36 cm²
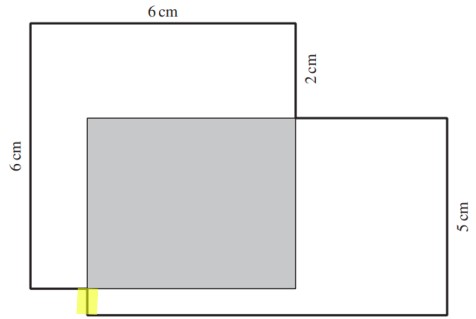
b) Berechne den Umfang der Gesamtfigur (in der Abbildung fett ausgezogen)
Berechne die Länge der gelb gefärbten Strecke.

- 1 cm
- 2 cm
- 0.5 cm
- 1.5 cm
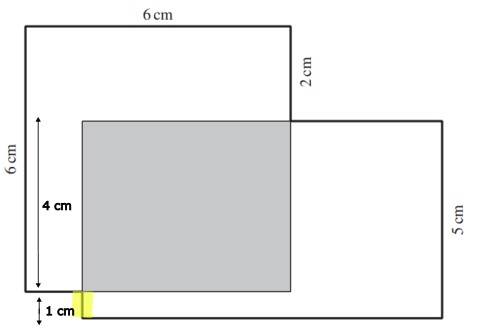
Die gelb markierte Strecke beträgt 1 cm.
Um die gelb markierte Strecke zu berechnen brauchst du zuerst die Breite des grauen Rechtecks. Diese beträgt 4 cm.
Damit rechnest du folgendermassen weiter:
1 cm (gelb markierte Strecke) + 4 cm (Breite graues Rechteck) = 5 cm (Breite des grossen Rechtecks)
Berechne die Länge der gelb gefärbten Strecke.
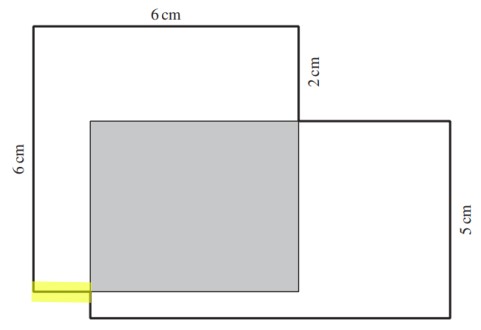

- 1 cm
- 2 cm
- 1.5 cm
- 3 cm
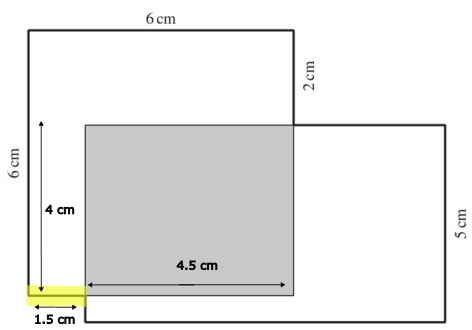
Die gelb markierte Strecke beträgt 1.5 cm.
Das berechnest du folgendermassen:
Das graue Rechteck hat eine Breite von 4 cm und einen Flächeninhalt von 18 cm².
Du weisst: Länge \(\cdot\) Breite = Flächeninhalt.
Länge des grauen Rechtecks: 18 cm² : 4 cm = 4.5 cm
6 cm - 4.5 cm = 1.5 cm
Berechne die Länge der gelb gefärbten Strecke.
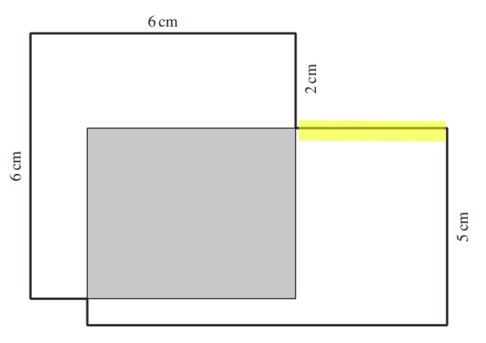

- 1.5 cm
- 2.7 cm
- 2 cm
- 3 cm
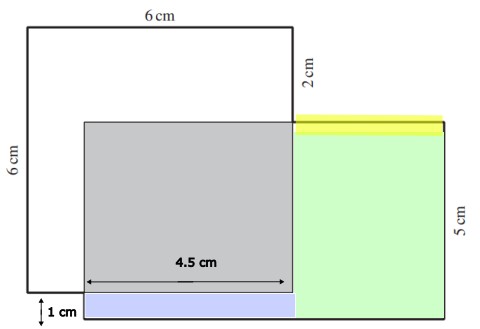
Die gelb markierte Strecke beträgt 2.7 cm.
Du berechnest die Länge in zwei Schritten:
Den Flächeninhalt des blau eingefärbten Rechtecks kennst du schon. Er beträgt 1 \(\cdot\) 4.5 cm, also 4.5 cm².
Insgesamt muss die Figur einen Flächeinhalt von 18 cm² haben (da der Flächeninhalt aller drei Teilfiguren gleich gross ist).
18 cm² - 4.5 cm² = 13.5 cm² muss der Flächeninhalt der restlichen Figur (grün) sein.
Schau dir nun das grüne Rechteck genauer an: Seine Seitenlänge ist 5 cm, sein Flächeninhalt ist 13.5 cm². Wie gross ist seine Breite (die gelb markierte Strecke)?
13.5 cm² : 5 cm = 2.7 cm
Was ist der Umfang der Gesamtfigur?
- 31.4 cm
- 35.4 cm
- 27.4 cm
- 39.4 cm
6 + 6 + 1.5 + 1 + 4.5 + 2.7 + 5 + 2.7 + 2 = 31.4 cm
Endresultat
- 42.4 cm
- 31.4 cm
- 29.4 cm
- 25.4 cm
- 42.4 cm
- 35.4 cm
- 27.4 cm
- 39.4 cm
