5.
Das Folgende ist eine Konstruktionsaufgabe. Drucke die Aufgabe aus und konstruiere mit Zirkel und Lineal. Bei jedem genutzten Tipp vervollständigt sich die Zeichnung in der Aufgabenstellung.
Der Wachhund Rex bewacht das grau schattierte Haus, neben dem der Wanderweg w vorbeiführt. Beim Punkt F hat Rex seinen Futternapf und beim Punkt K hat er einen Knochen vergraben.
a) Rex' Lieblingsplatz P befindet sich auf dem Wanderweg w und ist gleich weit vom Futternapf F und vom Knochen K entfernt. Konstruiere diesen Punkt P.
b) Rex ist angeleint. Seine Leine ist im Punkt L befestigt und hat eine Länge von 20 m. Der Massstab ist in der Figur angegeben. Weil Rex angeleint ist, kann er nicht jeden Punkt auf dem Gelände erreichen. Konstruiere und markiere das Gebiet, das Rex erreichen kann.
Gib als Endreultat das Folgende an: Bei welcher Koordinate liegt der Punkt P ungefähr? Bei welcher Koordinate schneidet das Gebiet, das Rex zugänglich ist, die linke Hauswand?
Der Wachhund Rex bewacht das grau schattierte Haus, neben dem der Wanderweg w vorbeiführt. Beim Punkt F hat Rex seinen Futternapf und beim Punkt K hat er einen Knochen vergraben.
a) Rex' Lieblingsplatz P befindet sich auf dem Wanderweg w und ist gleich weit vom Futternapf F und vom Knochen K entfernt. Konstruiere diesen Punkt P.
b) Rex ist angeleint. Seine Leine ist im Punkt L befestigt und hat eine Länge von 20 m. Der Massstab ist in der Figur angegeben. Weil Rex angeleint ist, kann er nicht jeden Punkt auf dem Gelände erreichen. Konstruiere und markiere das Gebiet, das Rex erreichen kann.
Gib als Endreultat das Folgende an: Bei welcher Koordinate liegt der Punkt P ungefähr? Bei welcher Koordinate schneidet das Gebiet, das Rex zugänglich ist, die linke Hauswand?
Der Punkt P liegt auf w und ist gleich weit vom Punkt F und Punkt K entfernt. Bei welcher Koordinate liegt P ungefähr?
- (5|11)
- (7|10)
- (9|10)
- (5|9)
Um P zu finden musst du die Punkte F und K verbinden. Anschliessend musst du diese Linie mithilfe einer Mittelsenkrechte halbieren.
Die Koordinaten von P setzen sich so zusammen: (x Koordinate | y Koordinate)
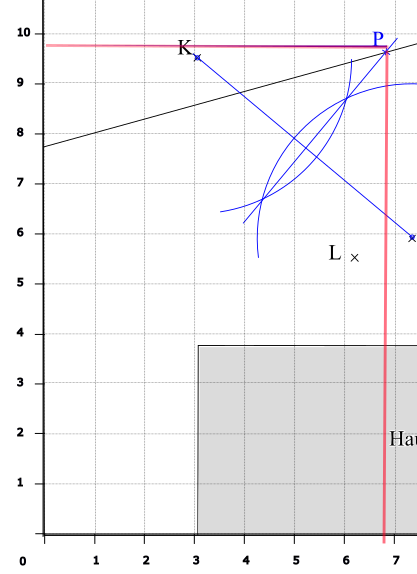
In der oberen Ecke der Zeichnung siehst du, wie lange 10 m sind. Wie lang sind 20 m ungefähr?
- Zwischen 5 und 6 Häuschen
- Zwischen 4 und 5 Häuschen
- Zwischen 10 und 30 Häuschen
- Zwischen 6 und 7 Häuschen
20 m sind doppelt so viel wie 10 m. Somit sind 20 m zwischen 5 und 6 Häuschen lang.
Nimm 20 m in den Zirkel. Wo musst du den Zirkel einstecken, um den Kreis abzutragen?
- Bei Punkt F
- Bei Punkt P
- An der rechten Ecke des Hauses
- Bei Punkt L
Da sich Rex nicht mehr als 20 m vom Punkt L entfernen kann, musst du den Zirkel dort einstecken. Der Kreis zeigt die Grenzen des Gebiets, das Rex erreichen kann.
Achtung: Wenn sich Rex links neben dem Haus bewegt, wird seine Leine um die Hausecke geknickt. Berücksichtige das in deiner Konstruktion. Bei welcher Koordinate schneidet das Gebiet, das Rex zugänglich ist, die linke Hauswand?
- (2|4)
- (3|2)
- (3|3)
- (3|1)
Um den Punkt zu finden, wo das Gebiet, das Rex zugänglich ist, die linke Hauswand schneidet:
1) Verbinde den Punkt L mit der Hausecke, wo die Leine geknickt wird.
2) Stich mit dem Zirkel bei der Hausecke ein.
3) Wie viel Leine ist noch übrig? Nimm die Distanz bis zum 20 Meter-Kreis in den Zirkel und zeichne einen neuen, kleineren Kreis.
4) Der kleinere Kreis schneidet die Hauswand im Punkt (3|2)
Schau dir die Zeichnung in der Aufgabenstellung an, um die Lösung und den Lösungsweg zu sehen.
Endresultat
- P = (7|10), Hauswand-Schnittpunkt = (3|2)
- P = (5|11), Hauswand-Schnittpunkt = (2|4)
- P = (9|10), Hauswand-Schnittpunkt = (3|3)
- P = (5|9), Hauswand-Schnittpunkt = (3|1)
- P = (5|11), Hauswand-Schnittpunkt = (3|1)
- P = (7|10), Hauswand-Schnittpunkt = (3|2)
- P = (9|10), Hauswand-Schnittpunkt = (3|3)
- P = (5|9), Hauswand-Schnittpunkt = (3|2)
