1.
Gib das Ergebnis an: (\(12.32 \cdot 56) - 100.8 + (19 \cdot 4.2) + (56 \cdot 7.68\))
Wenn du geschickt rechnest, kannst du den Rechenaufwand stark verringern.
Wenn du geschickt rechnest, kannst du den Rechenaufwand stark verringern.
(\(12.32 \cdot 56)\) \(- 100.8\) + \(19 \cdot\ 4.2)\) + (\(56 \cdot 7.68)\)
Schau dir die blau markierten Operationen an. Du siehst: In beiden Fällen wird mit 56 multipliziert. Was kann hier vereinfacht werden? Schau dir die blau markierten Operationen an. Du siehst: In beiden Fällen wird mit 56 multipliziert. Was kann hier vereinfacht werden?
Schau dir die blau markierten Operationen an. Du siehst: In beiden Fällen wird mit 56 multipliziert. Was kann hier vereinfacht werden? Schau dir die blau markierten Operationen an. Du siehst: In beiden Fällen wird mit 56 multipliziert. Was kann hier vereinfacht werden?
- ...Man kann \(56 \cdot (12.32\) + \(7.68)\) rechnen
- ...Man kann \(56 \cdot (12.32\) - \(7.68)\) rechnen
- ...Man muss beides einzeln ausrechnen, also \(12.32 \cdot 56\) und \(56 \cdot 7.68\)
- ...Man kann die 56 streichen und einfach mit 12.32 und 7.68 weiter rechnen
Man kann \(56 \cdot (12.32\) + \(7.68)\) rechnen
12.32 + 7.68 = 20
\(56 \cdot 20\) = 1120
Visuell dargestellt sieht das so aus:
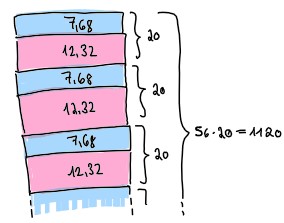
1120 - 100.8 + \((19 \cdot 4.2)\)
In der markierten Operation kann ein Trick angewandt werden:
In der markierten Operation kann ein Trick angewandt werden:
- Man kann \(19 \cdot 5\) rechnen und dann das Resultat - 0.8
- Man kann \(20 \cdot 4.2\) rechnen und dann das Resultat - 4.2
- Es gibt keinen Trick
- Man kann \(19 \cdot 5\) rechnen und dann das Resultat - 19
Man kann \(20 \cdot 4.2\) rechnen und dann das Resultat -\(4.2\)
\(20 \cdot 4.2 = 84\)
\(84\) - \(4.2 = 79.8\)
Der Grund dafür: 20 Mal eine 4.2 ist dasselbe wie 19 Mal 4.2 plus 4.2
Der letzte Schritt kann vereinfacht werden. Was ist das Endresultat?
- 1240
- 1230
- 1099
- 2000
1120 - 100 + 79
So kannst du das Endresultat berechnen.
Endresultat
- 1101
- 1100
- 1079
- 1089
- 1240
- 1230
- 1099
- 2000
