3.
a) Du siehst zwei Abbildungen mit Rechtecken, deren Seiten auf den Linien der Häuschen
liegen. Darin ist je eine Figur grau eingezeichnet. Welchem Bruchteil des Rechtecks entspricht jeweils der graue Teil? Gib deine Antwort als vollständig gekürzten Bruch an.
Markiere die Antworten für A und B deutlich.
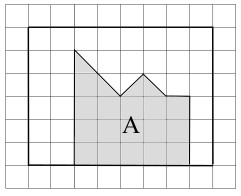
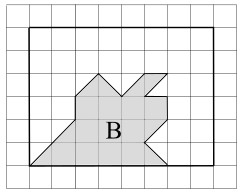


Die Rechtecke, welche die Figuren A und B enthalten sind gleich gross. Wie viele Häuschen enthalten diese Rechtecke?
- 54 Häuschen
- 45 Häuschen
- 35 Häuschen
- 48 Häuschen
Flächeninhalt eines Rechtecks = Länge \(\cdot\) Breite
In diesem Fall: 8 Häuschen \(\cdot\) 6 Häuschen = 48 Häuschen²
Wie viele Häuschen enthält die Figur A?
- 18 Häuschen
- 16 Häuschen
- 19 Häuschen
- 15 Häuschen
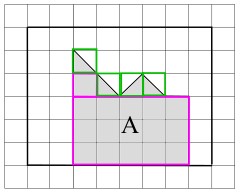
die Figur lässt sich in zwei Teile aufteilen. In rosa die vollständigen Häuschen. Davon gibt es 16.
Die halbierten Häuschen sind in grün umrandet. Es gibt 4 halbierte Häuschen, die sich zu 2 vollständigen Häuschen zusammensetzen lassen.
16 + 2 = 18 Häuschen in Figur A.
Welchem Bruchteil des Rechtecks entspricht die Figur A (ungekürzt)?
- 42/8
- 48/6
- 18/48
- 48/18
Rechteck: 48 Häuschen
Figur A: 18 Häuschen
Bruchteil: 18/48
Kürze den Bruch 18/48
- 2/5
- 1/6
- 5/7
- 3/8
Um einen Bruch zu kürzen dividierst du den Zähler und den Nenner durch dieselbe Zahl. Der Wert des Bruchs bleit unverändert.
Beispiel:
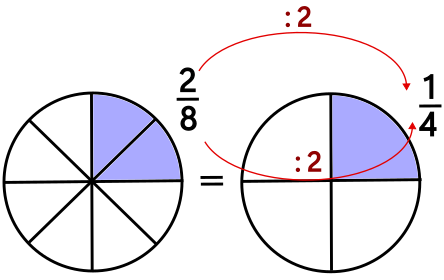
In diesem Fall:
18/48 = 3/8 (Zähler und Nenner durch 6 geteilt)
Wie viele Häuschen enthält die Figur B?
- 24 Häuschen
- 20 Häuschen
- 12 Häuschen
- 15 Häuschen
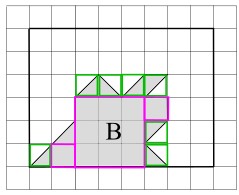
die Figur lässt sich in zwei Teile aufteilen. In rosa die vollständigen Häuschen. Davon gibt es 11.
Der zweite Teil besteht aus 8 halben Häuschen (grün). Das sind 4 ganze Häuschen.
11 + 4 = 15 Häuschen in Figur B.
Welchem Bruchteil des Rechtecks entspricht die Figur B (ungekürzt)?
- 45/15
- 48/15
- 20/48
- 15/48
Rechteck: 48 Häuschen
Figur B: 15 Häuschen
Bruchteil: 15/48
Kürze den Bruch 15/48
- 5/16
- 1/26
- 5/20
- 4/15
Um einen Bruch zu kürzen dividierst du den Zähler und den Nenner durch dieselbe Zahl. Der Wert des Bruchs bleit unverändert.
Beispiel:

In diesem Fall:
15/48 = 5/16 (Zähler und Nenner durch 3 geteilt)
Endresultat
- Bruchteil A = 3/8, Bruchteil B = 4/15
- Bruchteil A = 1/9, Bruchteil B = 1/6
- Bruchteil A = 3/8, Bruchteil B = 5/16
- Bruchteil A = 2/5, Bruchteil B = 1/2
- Bruchteil A = 5/7, Bruchteil B = 5/16
- Bruchteil A = 2/5, Bruchteil B = 1/6
- Bruchteil A = 3/8, Bruchteil B = 2/5
- Bruchteil A = 5/7, Bruchteil B = 4/15
b) Nun ist nur das Teilstück gezeichnet, das 2/5 von einem Rechteck ausmachen soll. Berechne
und notiere die Anzahl Häuschen des Rechtecks.
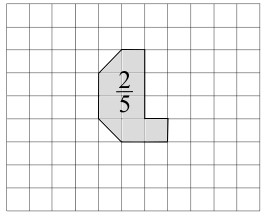

Wie viele Häuschen enthält das Teilstück?
- 8.5 Häuschen
- 9 Häuschen
- 12 Häuschen
- 8 Häuschen
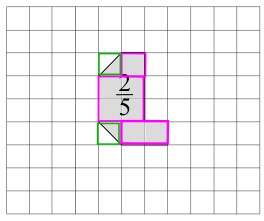
die Figur lässt sich in zwei Teile aufteilen. In rosa die vollständigen Häuschen. Davon gibt es 7.
Der zweite Teil besteht aus 2 halben Häuschen (grün). Das ist 1 ganzes Häuschen.
7 + 1 = 8 Häuschen in Figur C.
Wie viele Häuschen muss das Rechteck enthalten?
- 20 Häuschen
- 25 Häuschen
- 15 Häuschen
- 35 Häuschen
2/5 des Rechtecks → 8 Häuschen
1/5 des Rechtecks → 4 Häuschen (also 8 : 2)
5/5 des Rechtecks → 20 Häuschen (also 4 \(\cdot\) 5)
Das Rechteck muss 20 Häuschen enthalten.
Endresultat
- 20 Häuschen
- 25 Häuschen
- 35 Häuschen
- 15 Häuschen
- 25 Häuschen
- 24 Häuschen
- 36 Häuschen
- 48 Häuschen
