7.
Die folgende Figur (nicht massstäblich) ist aus Rechtecken zusammengesetzt.
Der Punkt E liegt in der Mitte zwischen B und F. Die Strecken AB und CD sind gleich lang. Der schattierte Teil hat die Fläche 63 cm².
Bestimme die Fläche der gesamten Figur (fett ausgezogen).
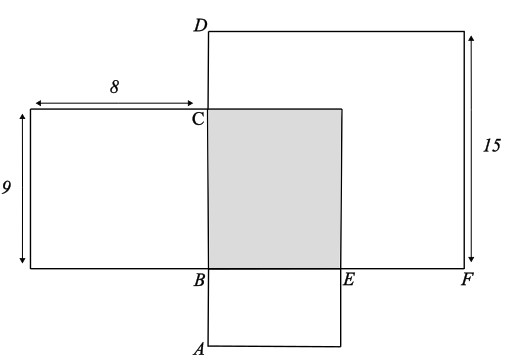
Bestimme die Fläche der gesamten Figur (fett ausgezogen).

Diese Art von Aufgabe ist wie ein Puzzle: Jede zusätzliche Information hilft dir, weiter voranzukommen
Wie lange ist die markierte Strecke?
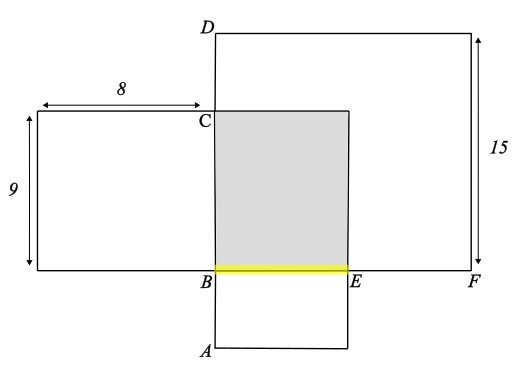
Wie lange ist die markierte Strecke?

- 7 cm
- 3 cm
- 9 cm
- 8 cm

Der Flächeninhalt des schraffierten Rechtecks beträgt 63 cm².
Seine Länge ist in der Abbildung gegeben und beträgt 9 cm.
63 cm² : 9 cm = 7 cm
Wie lang sind die beiden gelb markierten Strecken?
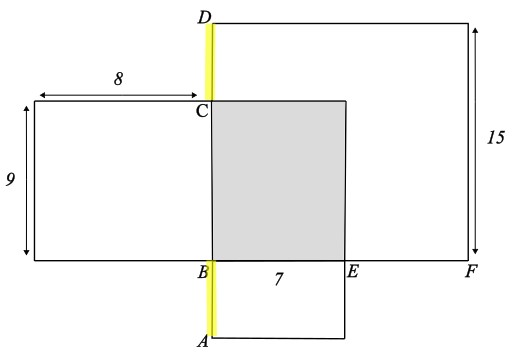

- 5 cm
- 4 cm
- 6 cm
- 7 cm
Die beiden Strecken sind gleich lang (das ist in der Aufgabenstellung gegeben)
Die Länge einer der gelben Strecken beträgt 15 cm - 9 cm = 6 cm
Was ist der Flächeninhalt des gelb markierten Rechtecks?
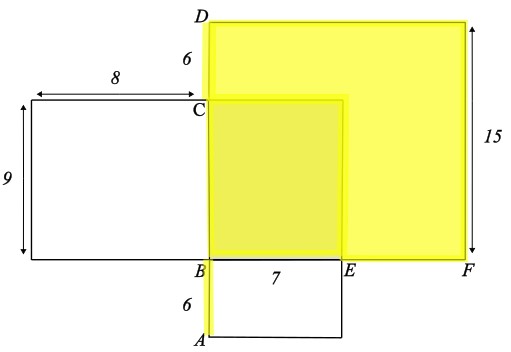

- 200 cm²
- 150 cm²
- 130 cm²
- 210 cm²
Die Länge des Rechtecks beträgt 15 cm.
Die Breite des Rechtecks beträgt 14 cm (Weil die Strecken BE und EF gleich lang sind. 7 cm + 7 cm = 14 cm)
Der Flächeninhalt beträgt 14 cm \(\cdot\) 15 cm = 210 cm²
Berechne die Fläche des markierten Rechtecks.
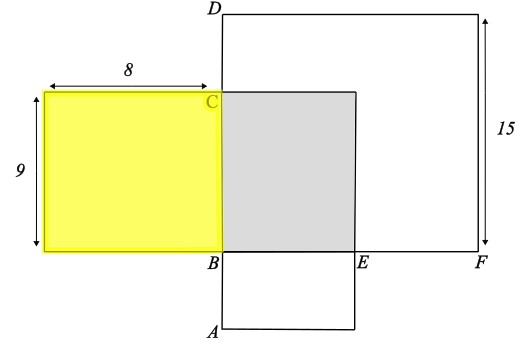

- 72 cm²
- 56 cm²
- 124 cm²
- 160 cm²
Die Länge des Rechtecks beträgt 9 cm.
Die Breite des Rechtecks beträgt 8 cm
Der Flächeninhalt beträgt 9 cm \(\cdot\) 8 cm = 72 cm²
Berechne die Fläche des markierten Rechtecks.
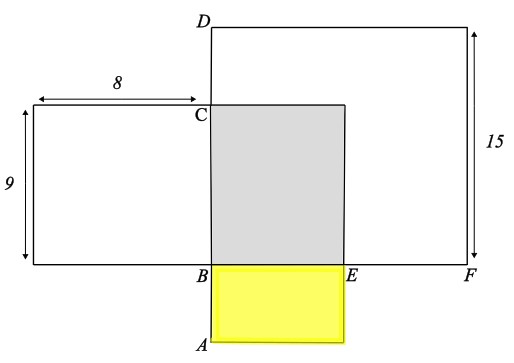

- 35 cm²
- 42 cm²
- 65 cm²
- 55 cm²
Die Länge des Rechtecks beträgt 7 cm.
Die Breite des Rechtecks beträgt 6 cm
Der Flächeninhalt beträgt 7 cm \(\cdot\) 6 cm = 42 cm²
Berechne die Fläche der gesamten Figur.
- 340 cm²
- 466 cm²
- 232 cm²
- 324 cm²
42 cm² + 72 cm² + 210 cm² = 324 cm²
Endresultat
- 340 cm²
- 286 cm²
- 345 cm²
- 466 cm²
- 401 cm²
- 324 cm²
- 316 cm²
- 232 cm²
