9.
Das folgende ist eine Geometriaufgabe mit Konstruktion. Jedes Mal wenn du einen Tipp nutzt, wird der Lösungsweg des Schrittes im untenstehenden Koordinatensystem eingetragen. Gib als Endresultat die Koordinaten von E an.
Konstruiere ein Fünfeck ABCDE mit den folgenden Eigenschaften:
• Das Fünfeck ABCDE ist achsensymmetrisch. Die Symmetrie-achse geht wie in der unten dargestellten Figur durch die Ecke C.
• Die Punkte A und B sind vorgegeben.
• Die Punkte C und D liegen auf der Geraden g.
• Die Länge der Strecke BC ist vorgegeben
• Der Winkel bei C ist stumpf (grösser als 90°)
Konstruiere ein Fünfeck ABCDE mit den folgenden Eigenschaften:
• Das Fünfeck ABCDE ist achsensymmetrisch. Die Symmetrie-achse geht wie in der unten dargestellten Figur durch die Ecke C.
• Die Punkte A und B sind vorgegeben.
• Die Punkte C und D liegen auf der Geraden g.
• Die Länge der Strecke BC ist vorgegeben
• Der Winkel bei C ist stumpf (grösser als 90°)
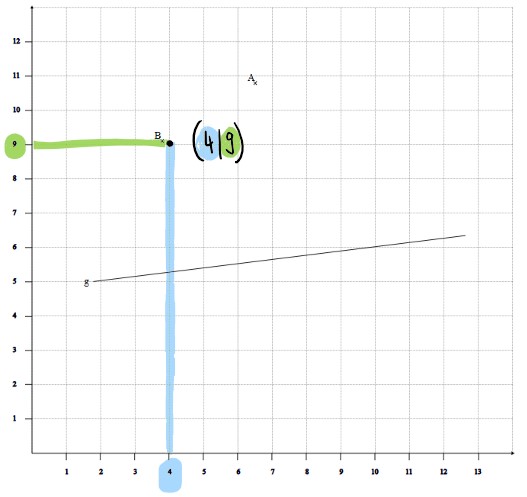
Verbinde A und B. Bei welcher Koordinate liegt B (ungefähr)?
- (9|4)
- (3|8)
- (4|9)
- (6|11)
B liegt am nächsten bei der (4|9) Koordinate. Als Erinnerung: Koordinaten kannst du so ablesen:
(Koordinate der x-Achse | Koordinate der y-Achse)
Schau dir das Zwischenresultat im obenstehenden Koordinatensystem an.
Bei welcher Koordinate liegt der Punkt C (ungefähr)?
- (5|2)
- (7.5|8)
- (2|5)
- (6.3|5.5)
Die Länge der Strecke BC ist vorgegeben. Nimm die Strecke in den Zirkel. Stich mit dem Zirkel bei B ein und schlage einen Bogen, der die Gerade g schneidet. C liegt bei einem der Schnittpunkte.
C liegt bei der Koordinate (6.3|5.5), weil D auch auf der Gerade g liegen muss und C einen stumpfen Winkel haben muss (beides ist in der Aufgabenstellung vorgegeben).
Bei welcher Koordinate liegt der Punkt E (ungefähr)?
Tipp: Finde dafür zuerst den Punkt D.
Tipp: Finde dafür zuerst den Punkt D.
- (10|9)
- (8|10)
- (10|7)
- (8|7.5)
Finde zuerst den Punkt D:
Wie die kleine Zeichnung in der oberen Ecke der Aufgabenstellung zeigt, verläuft eine Symmetrieachse durch C und die Mitte des Fünfecks. Die Länge CD ist somit gleich lang wie die Strecke BC.
Stich mit dem Winkel bei C ein, nimm die Strecke BC in den Zirkel ein und schlage einen Bogen der die Gerade g schneidet. Bei diesem Schnittpunkt liegt der Punkt D.
Um E zu finden:
Wegen der Symmetrie muss der Winkel bei D gleich gross sein wie der Winkel bei B. Trage den Winkel bei B ab und konstruiere ihn bei D.
Verbinde A und E. Das Fünfeck ist nun vervollständigt. Wo liegt die Koordinate E?
Endresultat
- (7|8)
- (9|10)
- (10|9)
- (6|9)
- (3|6)
- (11|8)
- (11|12)
- (12|9)
