1.
a) In der Rechenmaschine wird die eingegebene Zahl Schritt für Schritt verarbeitet:
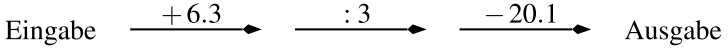
Welche Zahl musst du eingeben, damit die Ausgabezahl 102 herauskommt?
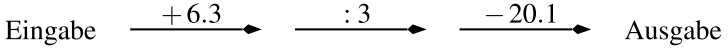
Welche Zahl musst du eingeben, damit die Ausgabezahl 102 herauskommt?
Die Ausgabezahl soll 102 betragen, die Eingabezahl ist unbekannt.
Beginne mit der Ausgabezahl und rechne rückwärts. Was ist dein erstes Zwischenresultat?
Beginne mit der Ausgabezahl und rechne rückwärts. Was ist dein erstes Zwischenresultat?
- 81.9
- 122.1
- 120.1
- 122.9

102 + 20.1 = 122.1
Das erste Zwischenresultat beträgt 122.1. Damit musst du weiter rückwärtsrechnen.
- 360.6
- 160.3
- 40.7
- 366.3
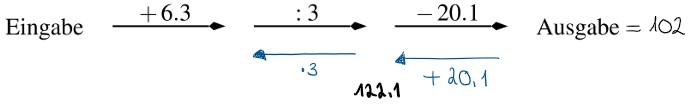
122.1 \(\cdot\) 3 = 366.3
Das zweite Zwischenresultat beträgt 366.3. Damit musst du weiter rückwärtsrechnen, um das Endresultat herauszufinden.
- 412
- 230
- 372
- 360

366.3 - 6.3 = 360
Endresultat
- 47
- 57
- 380
- 400
- 360
- 460
- 320
- 330
b) Rechne geschickt. Berechne mit möglichst wenig Rechenaufwand.
Schreibe deine Rechenschritte auf.
125 \(\cdot\) 6.408
Schreibe deine Rechenschritte auf.
125 \(\cdot\) 6.408
Statt mit 125 zu multiplizieren, kannst du mit 1000 multiplizieren. Dabei erhälst du natürlich ein falsches Resultat.
Überlege Dir, wie sich dieses falsche Resultat vom richtigen Resultat unterscheidet.
Überlege Dir, wie sich dieses falsche Resultat vom richtigen Resultat unterscheidet.
- Es ist um 75 zu gross
- Es ist 4 Mal grösser
- Es ist 8 Mal grösser
- Es ist um 125 zu gross
Weil du mit 1000 statt mit 125 multipliziert hast und weil 1000 = 8 \(\cdot\) 125 ist, ist unser falsches Resultat 8 Mal so gross wie das richtige Resultat.
Du musst also nur noch durch 8 teilen um auf die Lösung zu kommen.
1000 \(\cdot\) 6.408 = 6408
6408 : 8 = 801
Endresultat
- 901
- 800
- 790
- 830
- 900
- 806
- 801
- 890
